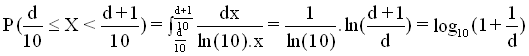
Dans trois séries de nombres décrites ci-dessous, on a relevé la distribution des fréquences du "chiffre significatif" qui est le premier chiffre non nul lu dans l'écriture de ce nombre en base 10 (le chiffre significatif de 2543,34 est 2 et celui de 0,00678 est 6).
- La colonne La bourse est relative à une série de 1000 nombres extraits des pages "finances et marchés" du journal Le Monde daté du vendredi 23 avril 1999. Ces nombres sont les taux de change des monnaies, les cours des matières premières en dollars ou en euros, les prix des actions dans différents domaines : automobile, banques, chimie, pharmacie, télécommunications ...Le plus petit nombre correspond au taux d'échange franc contre livre sterling (valeur : 0,101 05) et le plus grand au prix en dollars de l'once de platine (valeur : 81 602,53).
- Les 1229 nombres qui ont servi dans la colonne Recensement sont relatifs au recensement national de 1992. Les données représentent le nombre d'habitants de chaque commune de l'Isère et du Vaucluse, les derniers nombres donnant la population totale de tous les départements et celle de la France. Le plus petit nombre (valeur : 9) correspond à la population de la commune de Oulles (Isère); et le plus grand (valeur : 58 0730553) à la population totale de la France.
Les 914 chiffres de la colonne Gilibert sont extraits des
colonnes débits et crédits d'un historique de compte de
la société Gilibert, une société de
fabrication de remorques, pour l'année 1995. Ils ont diverses
origines : frais de minitel, cotisations ASSEDIC, achat de gasoil,
payements de clients, cotisations à la
médecine du travail, impôts... Le plus grand nombre
correspond à un total des débits du 10/01/95 au 30/09/95
(valeur : 96 981 060,08), et le plus petit à la fin de
règlement d'un compte (valeur : 0,03).
|
Premier chiffre |
La bourse |
Recensement |
Gilibert |
|
1 |
0,322 |
0,321 |
0,317 |
|
2 |
0,151 |
0,168 |
0,161 |
|
3 |
0,108 |
0,133 |
0,142 |
|
4 |
0,099 |
0,081 |
0,088 |
|
5 |
0,073 |
0,087 |
0,070 |
|
6 |
0,081 |
0,067 |
0,061 |
|
7 |
0,055 |
0,055 |
0,070 |
|
8 |
0,065 |
0,045 |
0,040 |
|
9 |
0,046 |
0,044 |
0,050 |
On observe là un phénomène étonnant : ces distributions de fréquences sont très voisines !
Un tel phénomène mérite une explication.
Pour la trouver, posons-nous deux questions.
En fait, on peut multiplier les nombres des trois colonnes par n'importe quelle quantité, on observe toujours à peu près la même distribution des fréquences : la propriété observée est invariante par changement d'échelle.
De même, si on écrit les nombres du tableau dans une autre base, les distributions des fréquences relatives aux trois séries restent encore voisines.
2- L'usure du premier volume des tables de logarithmes :
On peut lire dans un article de La Recherche (janvier 1999) ayant pour titre Le premier chiffre significatif fait sa loi, les faits ci-dessous.
En 1881, Simon Newcomb publie un article présentant un étrange phénomène : le premier volume des tables logarithmiques est plus utilisé que le deuxième qui l'est plus que le troisième et ainsi de suite. Un savant calcul l'amène à conclure que la probabilité que le premier chiffre significatif d'un nombre, " pris dans un ensemble quelconque ", soit d, est égale à log10(1+1/d). Cet article passe totalement inaperçu.
Par contre, 57 ans plus tard, un article de Franck Benford, motivé par la même observation et aboutissant à la même loi de probabilité, étayé d'exemples éclectiques, attire l'attention. La loi est baptisée loi de Benford.
On a trouvé depuis de très nombreux exemples de données se conformant à cette loi de probabilité.
3- Mesures invariantes
Pour comprendre le phénomène observé, nous
allons nous interesser à certaines lois de probabilité
définies à partir de mesures invariantes.
3-1 Invariance par translation
On dit qu'une mesure m sur (R, B (R )) est invariante par translation si :
"B ÎB(R ), "a ÎR m(a+B) = m(B) où a+B = {a+b, bÎB}A un coefficient multiplicatif près, il y a unicité d'une telle mesure : c'est la mesure de Haar du groupe (R ,+). La mesure de Lebesgue dx est l'unique mesure m invariante par translation et telle que m([0,1]) = 1.
En projetant alors la mesure de Lebesgue sur {R /c.Z ,+}, où c ÎR , on obtient la mesure uniforme. Par normalisation on construit la loi de probabilité uniforme sur [0,c[, à savoir dx/c.
3-2 Invariance par changement d'échelle
On dit qu'une mesure m sur (R +*,B (R +*)) est invariante par changement d'échelle si :
"B ÎB (R ), "a ÎR m(a.B) = m(B) où a.B = {a.b, bÎB}A un coefficient multiplicatif près, il y a unicité d'une telle mesure : c'est la mesure de Haar du groupe (R +*, ´). La mesure dx/x est l'unique mesure invariante m telle que m([1,e]) = 1.
En
projetant m = dx/x sur (R
+*/cZ , ´), on obtient la mesure dx/x sur [1/c,1[ dont
nous nommerons la forme normalisée loi de Benford continue sur
[1/c,1[.
3-3 Lois de Benford discrètes
-Choisissons la base 10 (c =10).
Soit X une variable aléatoire suivant la loi de Benford sur [0,1 ;1 [.
Soit d Î {1,...,9}.
Alors, la probabilité que le premier chiffre significatif de X soit d est :
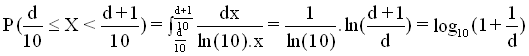
Donc si des
données
sont invariantes par changement d'échelle, leurs
premiers chiffres significatifs peuvent être considérés comme un
échantillon
de la loi définie sur {1,...,9} par :
que nous nommerons loi de Benford discrète en base 10.
Le même calcul montre que si on écrit les nombres en base c, c étant un entier supérieur à 2, alors la série des premiers chiffres significatifs en base c suivra la loi B(c), avec :
On notera que pour des valeurs élevées de i, PB(c)(i) est presque inversement proportionnel à i, et on retombe ainsi sur la loi de Zipf étudiée en linguistique.
-L'image de la mesure de Lebesgue dx par l'homomorphisme de groupe :
(R ,+) ® (R +*,´)
x ® ex
est la mesure dx/x sur R +*. L'image de la loi U[0,1[ par f : [0;1[ ® [1 ;10[ telle que f(x)=10x-1 est la loi de Benford continue sur [0,1;1[.
En particulier, pour simuler un
échantillon
de taille n de B10,
il suffit de prendre l'algorithme suivant :
Pour i Î{1, ..., n} :
X® random ([0;1[)
Y=10X
Ecrire Y
4- Petits calculs
4-1 Probabilités des cinq premiers chiffres
Le tableau suivant donne la probabilité
des cinq premiers chiffres significatifs
selon la loi de Benford ainsi que la
distance du chi-deux
de chaque colonne avec
la
loi uniforme
: 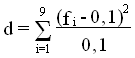 pour le
premier chiffre
puis
pour le
premier chiffre
puis 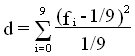 où fi est la
fréquence
du i-ème chiffre.
où fi est la
fréquence
du i-ème chiffre.
Le calcul des
probabilités
des chiffres dans l'ordre de leur lecture est
donné par :
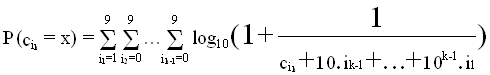
où ij est la valeur du j-ème chiffre significatif.
| x |
100.P(c1=x) |
100.P(c2=x) |
100.P(c3=x) |
100.P(c4=x) |
100.P(c5=x) |
| 0 | 12,0 | 10,18 | 10,02 | 10,00 | |
|
1 |
30,1 |
11,4 |
10,14 |
10,01 |
10,00 |
|
2 |
17,6 |
10,9 |
10,10 |
10,01 |
10,00 |
|
3 |
12,5 |
10,4 |
10,06 |
10,01 |
10,00 |
|
4 |
9,7 |
10,0 |
10,02 |
10,00 |
10,00 |
|
5 |
8,0 |
9,7 |
9,98 |
10,00 |
10,00 |
|
6 |
6,7 |
9,3 |
9,94 |
9,99 |
10,00 |
|
7 |
5,8 |
9,0 |
9,90 |
9,99 |
10,00 |
|
8 |
5,1 |
8,8 |
9,86 |
9,99 |
10,00 |
|
9 |
4,6 |
8,5 |
9,83 |
9,98 |
10,00 |
| chi-deux |
1,49 |
1,3.10-2 |
1,3.10-4 |
1,3.10-6 |
1,3.10-8 |
4-2 Probabilités conditionnelles du deuxième chiffre
Le tableau suivant donne (100 ´) la probabilité que le deuxième chiffre soit c2, sachant que le premier est c1.
Le calcul des probabilités conditionnelles est le suivant :
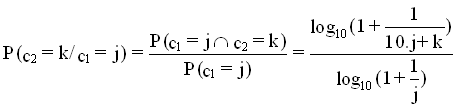
|
c1 c2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
13,8 |
12,0 |
11,4 |
11,0 |
10,9 |
10,7 |
10,6 |
10,5 |
10,5 |
|
1 |
12,6 |
11,5 |
11,0 |
10,8 |
10,7 |
10,5 |
10,5 |
10,4 |
10,4 |
|
2 |
11,5 |
11,0 |
10,7 |
10,5 |
10,4 |
10,4 |
10,3 |
10,3 |
10,3 |
|
3 |
10,7 |
10,5 |
10,4 |
10,3 |
10,3 |
10,2 |
10,2 |
10,2 |
10,2 |
|
4 |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
|
5 |
9,3 |
9,7 |
9,8 |
9,8 |
9,9 |
9,9 |
9,9 |
9,9 |
9,9 |
|
6 |
8,7 |
9,3 |
9,5 |
9,6 |
9,7 |
9,7 |
9,8 |
9,8 |
9,8 |
|
7 |
8,2 |
9,0 |
9,3 |
9,4 |
9,5 |
9,6 |
9,7 |
9,7 |
9,7 |
|
8 |
7,8 |
8,7 |
9,0 |
9,2 |
9,4 |
9,5 |
9,5 |
9,6 |
9,6 |
|
9 |
7,4 |
8,4 |
8,8 |
9,0 |
9,2 |
9,3 |
9,4 |
9,5 |
9,5 |
Reprenons les données pour la colonne recensement du §1 et testons l'hypothèse nulle que les chiffres significatifs suivent la loi de Benford .
La
statistique du chi-deux
pour chacune des colonnes du tableau du §1 est le produit de la
taille de
l'échantillon
par la distance de la distribution des
fréquences
à
la loi de Benford.
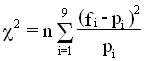 ,
,
où pi= Log10(1+1/i), et n est le nombre de données .
Les résultats sont les suivants :
|
n |
distance du chi-deux | |
|
La bourse |
1000 |
14,8 |
|
Recensement |
1229 |
7,9 |
|
Population |
914 |
11,03 |
Pour le test dont l'hypothèse nulle est que les chiffres significatifs suivent la loi de Benford, la valeur limite de rejet au seuil 5% est 15,5 ; on peut donc accepter l'hypothèse nulle pour les trois ensembles de données au risque 5%.
Pour mieux percevoir ce phénomène d'invariance d'échelle,
rien n'empêche de faire de nouvelles expériences : collecter des
données
analogues, calculer le chiffre significatif de ces
données
et des
données
multipliées par une constante, calculer la distance de la
distribution des
fréquences
à la loi de Benford, faire un
test du chi-deux.
ou d'autres tests pour tester
l'adéquation
à la loi de Benford continue, etc...
