La fonction quantile d'une variable aléatoire (ou d'une loi de probabilité) est l'inverse de sa fonction de répartition. Quand cette fonction de répartition est strictement croissante, son inverse est définie sans ambigüité. Mais une fonction de répartition reste constante sur tout intervalle dans lequel la variable aléatoire ne peut pas prendre de valeurs. C'est pourquoi on introduit la définition suivante.
Par convention, on peut décider que ![]() est la plus petite des valeurs
possibles pour
est la plus petite des valeurs
possibles pour ![]() et
et ![]() est la plus grande (elles sont éventuellement
infinies).
est la plus grande (elles sont éventuellement
infinies).
Lois discrètes.
La
fonction quantile
d'une variable aléatoire
discrète est une fonction en escalier, comme la
fonction de répartition.
Si ![]() prend les valeurs
prend les valeurs
![]() , rangées par ordre croissant,
la
fonction de répartition
est égale à :
, rangées par ordre croissant,
la
fonction de répartition
est égale à :
![\begin{displaymath}
Q_X(u)=\left\{
\begin{array}{lcl}
x_1&&\mbox{pour } u\in ]0,...
...mbox{pour } u\in ]F_k,F_{k+1}]\\
&\vdots&
\end{array}\right.
\end{displaymath}](img429.gif)
Lois continues.
Plaçons-nous dans le cas le plus fréquent, où la
densité
![]() est strictement positive sur un intervalle de
est strictement positive sur un intervalle de
![]() (son
support) et nulle ailleurs. Si l'intervalle est
(son
support) et nulle ailleurs. Si l'intervalle est ![]() , la fonction de
répartition est nulle
avant
, la fonction de
répartition est nulle
avant ![]() si
si ![]() est fini, elle est strictement croissante de 0 à 1 entre
est fini, elle est strictement croissante de 0 à 1 entre
![]() et
et ![]() , elle vaut 1 après
, elle vaut 1 après ![]() si
si ![]() est fini. Toute valeur
est fini. Toute valeur ![]() strictement comprise entre 0 et 1 est prise une fois et une seule par
strictement comprise entre 0 et 1 est prise une fois et une seule par
![]() . La valeur de
. La valeur de ![]() est le point
est le point ![]() unique, compris entre
unique, compris entre ![]() et
et ![]() ,
tel que
,
tel que
![]() .
.
Calculons par exemple la
fonction quantile
de la
loi exponentielle
![]() , de
fonction de répartition
, de
fonction de répartition
![]() 1
1![]() . Pour tout
. Pour tout
![]() ,
,
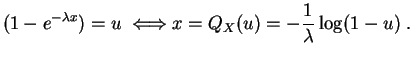
La
fonction quantile
est un moyen de décrire la dispersion d'une loi.
Si on réalise un grand nombre de tirages
indépendants
de la même loi
(un échantillon), on doit s'attendre à ce qu'une proportion
![]() des valeurs soient inférieures à
des valeurs soient inférieures à ![]() . Une valeur importante
est la
médiane
,
. Une valeur importante
est la
médiane
, ![]() . Les fonctions quantiles
sont souvent utilisées en
statistiques.
On calcule en particulier fréquemment des
intervalles de dispersion,
compris comme devant contenir
une forte proportion des
données.
. Les fonctions quantiles
sont souvent utilisées en
statistiques.
On calcule en particulier fréquemment des
intervalles de dispersion,
compris comme devant contenir
une forte proportion des
données.
En
statistiques,
les réels ![]() compris entre 0 et
1 sont de tradition. La même tradition leur affecte prioritairement les
valeurs
compris entre 0 et
1 sont de tradition. La même tradition leur affecte prioritairement les
valeurs ![]() et
et ![]() , plus rarement
, plus rarement ![]() ,
, ![]() ou
ou ![]() . Il
faut donc lire
. Il
faut donc lire ![]() comme "une faible proportion", et
comme "une faible proportion", et
![]() comme "une forte proportion". Un
intervalle de dispersion
de niveau
comme "une forte proportion". Un
intervalle de dispersion
de niveau
![]() pour
pour ![]() est tel que
est tel que ![]() appartient à cet intervalle avec
probabilité
appartient à cet intervalle avec
probabilité
![]() , il contient donc une forte proportion
de la
densité,
même s'il est en général beaucoup plus petit
que le support de la loi. Il existe en général une infinité
d'
intervalles de dispersion
de niveau donné. En voici quelques uns, de
niveau
, il contient donc une forte proportion
de la
densité,
même s'il est en général beaucoup plus petit
que le support de la loi. Il existe en général une infinité
d'
intervalles de dispersion
de niveau donné. En voici quelques uns, de
niveau ![]() pour la
loi normale
pour la
loi normale
![]() .
.
Selon les valeurs de ![]() , on dit qu'un
intervalle de dispersion
de niveau
, on dit qu'un
intervalle de dispersion
de niveau
![]() est :
est :
Une autre application importante de la fonction quantile est la méthode d'inversion qui est une méthode générale, consistant à simuler une variable aléatoire de loi quelconque, en composant un appel de Random avec sa fonction quantile.
Démonstration : Pour tout
Exemple : La
fonction quantile
de la
loi exponentielle
![]() associe à
associe à ![]() la valeur
la valeur
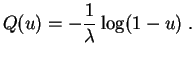
![]() Random
Random
![]()
(Il est inutile de calculer
![]() Random
Random
![]() car
Random
et
car
Random
et ![]() Random
suivent la même loi).
Random
suivent la même loi).
La méthode d'inversion n'est exacte qu'à condition de connaître
l'expression explicite de ![]() , comme pour la
loi exponentielle.
C'est
rarement le cas. Si on veut appliquer la méthode à la
loi normale
par
exemple, il faudra utiliser un algorithme d'approximation. En plus
de l'imprécision, la méthode d'inversion sera alors relativement lente.
Même quand on connaît explicitement
, comme pour la
loi exponentielle.
C'est
rarement le cas. Si on veut appliquer la méthode à la
loi normale
par
exemple, il faudra utiliser un algorithme d'approximation. En plus
de l'imprécision, la méthode d'inversion sera alors relativement lente.
Même quand on connaît explicitement ![]() , la méthode d'inversion
est rarement la plus efficace pour les
variables à densité.
Elle convient
par contre bien à de nombreuses loi discrètes.
, la méthode d'inversion
est rarement la plus efficace pour les
variables à densité.
Elle convient
par contre bien à de nombreuses loi discrètes.
Supposons que ![]() prenne les valeurs
prenne les valeurs
![]() , rangées par ordre
croissant. Notons
, rangées par ordre
croissant. Notons ![]() la valeur de la fonction
de répartition sur l'intervalle
la valeur de la fonction
de répartition sur l'intervalle
![]() . L'algorithme de simulation
par inversion est le suivant.
. L'algorithme de simulation
par inversion est le suivant.
![]()
![]() Random
Random
TantQue (![]() ) faire
) faire
![]()
finTantQue
![]()
Modifions légèrement cet l'algorithme en lui rajoutant une
interpolation linéaire. Quand ![]() tombe dans
l'intervalle
tombe dans
l'intervalle
![]() , au lieu de retourner
, au lieu de retourner ![]() comme
précédemment, nous retournons :
comme
précédemment, nous retournons :
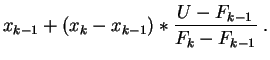
Ceci revient à remplacer la
fonction de répartition
en escalier par une
fonction de répartition
linéaire par morceaux, passant par les points
![]() . La distribution de
probabilité
correspondante admet pour
densité
une fonction en escalier (constante sur les intervalles
. La distribution de
probabilité
correspondante admet pour
densité
une fonction en escalier (constante sur les intervalles
![]() ). C'est un
histogramme.
). C'est un
histogramme.