On démontre que l'existence de la
variance
entraîne celle de
l'espérance.
Par contre une
variable aléatoire
![]() peut très bien avoir une
espérance
mais pas de
variance.
C'est le cas par exemple si
peut très bien avoir une
espérance
mais pas de
variance.
C'est le cas par exemple si ![]() a pour
densité
:
a pour
densité
:
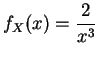 1
1
Démonstration : Pour passer de la définition à la formule ci-dessus, il suffit de développer le carré et d'utiliser la linéarité de l'intégrale.
La
variance
mesure de combien les valeurs prises par ![]() s'écartent de la
valeur moyenne
s'écartent de la
valeur moyenne
![]() . Elle n'est pas homogène : si
. Elle n'est pas homogène : si ![]() est une longueur
exprimée en mètres,
est une longueur
exprimée en mètres, ![]() est en mètres-carrés. On corrige
ceci en introduisant
l'écart-type
qui est la racine carrée de la
variance.
Les propriétés principales de la
variance
sont les suivantes.
est en mètres-carrés. On corrige
ceci en introduisant
l'écart-type
qui est la racine carrée de la
variance.
Les propriétés principales de la
variance
sont les suivantes.
Démonstration : Les deux premières propriétés sont des conséquences directes de la définition. Pour la troisième, si
L'inégalité de Bienaymé-Tchebichev ci-dessous
traduit l'idée intuitive que les valeurs prises par ![]() s'écartent d'autant moins de
s'écartent d'autant moins de
![]() que
que ![]() est plus faible.
Le cas extrême est celui d'une
variable aléatoire
de
variance
nulle,
qui ne peut prendre qu'une seule valeur.
est plus faible.
Le cas extrême est celui d'une
variable aléatoire
de
variance
nulle,
qui ne peut prendre qu'une seule valeur.
Démonstration : Nous démontrons ce résultat pour les variables continues, le raisonnement pour les variables discrètes est analogue. Posons
![\begin{displaymath}
\begin{array}{l}
Var[X]= \displaystyle\int_{\mathbb{R}}(x-m)...
... \varepsilon^2P[\,\vert X-m\vert>\varepsilon\,] \;.
\end{array}\end{displaymath}](img560.gif)
Le tableau ci-dessous donne les variances des lois usuelles, discrètes et continues.