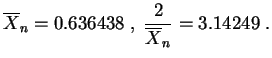L'idée de
l'estimation
par
intervalle de confiance
est de définir, autour
de la
moyenne empirique,
un intervalle
aléatoire
(dépendant des ![]() expériences) qui contienne
expériences) qui contienne ![]() avec une forte
probabilité.
C'est l'amplitude de cet intervalle qui mesure la précision
de
l'estimation.
avec une forte
probabilité.
C'est l'amplitude de cet intervalle qui mesure la précision
de
l'estimation.
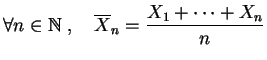 et
et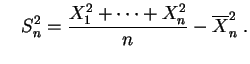
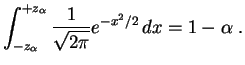
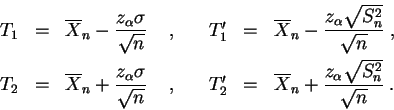
Alors :
On dit que les intervalles
aléatoires
![]() et
et
![]() sont
des
intervalles de confiance
pour
sont
des
intervalles de confiance
pour ![]() , de niveau de confiance asymptotique
, de niveau de confiance asymptotique
![]() .
.
Interprétation
La valeur ![]() étant inconnue, il n'y a pas de raison a priori pour que
l'écart-type
étant inconnue, il n'y a pas de raison a priori pour que
l'écart-type
![]() soit connu. S'il est inconnu, on l'estime par
l'écart-type empirique
soit connu. S'il est inconnu, on l'estime par
l'écart-type empirique
![]() . C'est la raison pour laquelle
nous donnons deux
intervalles de confiance.
La valeur de
. C'est la raison pour laquelle
nous donnons deux
intervalles de confiance.
La valeur de ![]() est lue dans une table, ou retournée par un module
de calcul numérique. Les valeurs les plus courantes sont les suivantes :
est lue dans une table, ou retournée par un module
de calcul numérique. Les valeurs les plus courantes sont les suivantes :
Les intervalles ![]() et
et
![]() sont
aléatoires.
A l'issue de la série de
sont
aléatoires.
A l'issue de la série de ![]() expériences,
expériences, ![]() et
et ![]() auront pris des valeurs particulières
auront pris des valeurs particulières ![]() et
et ![]() .
L'encadrement
.
L'encadrement
![]() sera alors
vrai ou faux. Pour
sera alors
vrai ou faux. Pour
![]() , si on répète
, si on répète ![]() fois la série de
fois la série de ![]() expériences pour obtenir
expériences pour obtenir ![]() intervalles,
on peut s'attendre à ce que cinq d'entre eux ne contiennent
pas
intervalles,
on peut s'attendre à ce que cinq d'entre eux ne contiennent
pas ![]() .
.
Il faut comprendre un
intervalle de confiance
comme une précision
donnée sur la valeur estimée de ![]() :
:
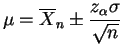 ou
ou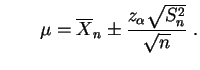
Estimation d'une probabilité.
Supposons que la quantité à estimer soit la
probabilité
![]() d'un
évènement. On réalise une suite d'expériences
indépendantes, en
notant à chaque fois si l'évènement est réalisé (1) ou non (0).
La
variable aléatoire
correspondant à la
d'un
évènement. On réalise une suite d'expériences
indépendantes, en
notant à chaque fois si l'évènement est réalisé (1) ou non (0).
La
variable aléatoire
correspondant à la ![]() -ième expérience est
notée
-ième expérience est
notée ![]() . Les
. Les ![]() suivent la
loi de Bernoulli
de paramètre
suivent la
loi de Bernoulli
de paramètre ![]() .
.
Reprenons l'expérience de l'aiguille de Buffon, consistant à lancer au
hasard une aiguille sur un
parquet. Si la largeur des lames est égale à la longueur de l'aiguille,
nous avons vu que la
probabilité
(théorique) pour que
l'aiguille tombe à cheval sur 2 lames de parquet est ![]() .
Supposons que l'on répète
.
Supposons que l'on répète ![]() fois l'expérience, physique ou par
simulation.
A l'issue des
fois l'expérience, physique ou par
simulation.
A l'issue des ![]() répétitions, on obtient une valeur de la
fréquence expérimentale
répétitions, on obtient une valeur de la
fréquence expérimentale
![]() et donc un
intervalle de confiance
et donc un
intervalle de confiance
![]() . L'intervalle
. L'intervalle
![]() est aussi un intervalle de
confiance pour la valeur
est aussi un intervalle de
confiance pour la valeur ![]() .
Voici par exemple des résultats obtenus sur
.
Voici par exemple des résultats obtenus sur ![]() expériences.
expériences.