Parmi les différentes formalisations du hasard qui ont pu être proposées, la notion de suite uniforme est la seule utilisable en pratique : elle est la seule que l'on puisse tester pour un générateur donné et elle suffit à justifier toutes les applications de la fonction Random. Une "vraie" suite aléatoire doit être uniforme. Mais peut-on considérer comme aléatoire toute suite uniforme ? Nous allons voir que non, malheureusement.
Comme l'ordinateur ne peut donner que des approximations décimales des
réels, il suffirait de savoir construire une
suite aléatoire
de
chiffres entre 0 et ![]() , pour en déduire des réels
au hasard
dans
, pour en déduire des réels
au hasard
dans
![]() , approchés à la
, approchés à la ![]() -ème décimale, en considérant des
-ème décimale, en considérant des
![]() -uplets consécutifs de chiffres de la suite initiale. La même remarque
vaut bien sûr en base 2. Il suffirait donc de savoir définir ce qu'est
une suite de bits
au hasard.
-uplets consécutifs de chiffres de la suite initiale. La même remarque
vaut bien sûr en base 2. Il suffirait donc de savoir définir ce qu'est
une suite de bits
au hasard.
Limitons-nous donc aux suites de bits dans ![]() .
On attend d'une telle suite qu'elle soit le résultat typique d'une suite
de tirages de
Pile ou Face.
Voici trois séquences particulières :
.
On attend d'une telle suite qu'elle soit le résultat typique d'une suite
de tirages de
Pile ou Face.
Voici trois séquences particulières :
La troisième a meilleur aspect que les deux premières. Elle a pourtant
exactement la même
probabilité
de sortir telle quelle à
Pile ou Face
:
![]() . Parmi les
. Parmi les ![]() -uplets de bits, tous ont a priori la même
probabilité
de sortir :
-uplets de bits, tous ont a priori la même
probabilité
de sortir :
![]() . Toute
suite aléatoire
de bits doit
contenir nécessairement une infinité de fois
. Toute
suite aléatoire
de bits doit
contenir nécessairement une infinité de fois ![]() zéros à la suite.
Accepterions-nous qu'un générateur de bits retourne ne serait-ce que
zéros à la suite.
Accepterions-nous qu'un générateur de bits retourne ne serait-ce que
![]() zéros à la suite ? Cela paraît peu vraisemblable.
zéros à la suite ? Cela paraît peu vraisemblable.
Sur les ![]() exemples ci-dessus, nous écarterions le premier car il semble
violer la 1-uniformité. Nous écarterions le second au nom de la
2-uniformité. Mais que dire alors de la suite concaténée de tous les
entiers en base 2 (suite de Champernowne) ?
exemples ci-dessus, nous écarterions le premier car il semble
violer la 1-uniformité. Nous écarterions le second au nom de la
2-uniformité. Mais que dire alors de la suite concaténée de tous les
entiers en base 2 (suite de Champernowne) ?
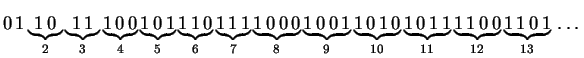
On montre qu'elle est ![]() -uniforme. Mais comment qualifier
d'aléatoire
une suite aussi parfaitement prévisible ?
-uniforme. Mais comment qualifier
d'aléatoire
une suite aussi parfaitement prévisible ?
La définition la plus intuitive du hasard, celle des dictionnaires, n'a
aucun rapport avec l'uniformité. Est
aléatoire
ce qui est imprévisible.
Une suite serait donc
aléatoire
si on ne pouvait pas prévoir son
![]() -ème terme connaissant les
-ème terme connaissant les ![]() premiers. La suite
premiers. La suite
On peut voir une règle de construction comme un moyen de compresser une suite en un algorithme qui l'engendre.
Exemple :
Répéter ![]() fois
fois
écrire 0 puis 1
finRépéter
Traduit en chaîne de bits, la seule chose qui dépend de ![]() dans cet
algorithme est le test. La longueur de la chaîne de bits sera
dans cet
algorithme est le test. La longueur de la chaîne de bits sera
![]() constante, pour engendrer à l'exécution une chaîne de
longueur
constante, pour engendrer à l'exécution une chaîne de
longueur ![]() (
(![]() est le nombre de bits nécessaires pour écrire
est le nombre de bits nécessaires pour écrire
![]() , à 1 près).
, à 1 près).
Notons ![]() l'ensemble de toutes les chaînes de bits de longueur finie.
Si
l'ensemble de toutes les chaînes de bits de longueur finie.
Si ![]() , sa longueur (nombre de bits) sera notée
, sa longueur (nombre de bits) sera notée ![]() . Un algorithme
est une application de
. Un algorithme
est une application de ![]() dans lui-même.
dans lui-même.
|
|
||
|
|
||
Soit
![]() la taille du codage de
la taille du codage de ![]() exprimée en bits
(hors input).
exprimée en bits
(hors input).
En d'autres termes
![]() est une mesure de la taille de l'information
qu'il faut donner à l'algorithme
est une mesure de la taille de l'information
qu'il faut donner à l'algorithme ![]() pour produire
pour produire ![]() . Dans l'exemple
ci-dessus, une chaîne de
. Dans l'exemple
ci-dessus, une chaîne de ![]() bits suffisait à produire la
chaîne de longueur
bits suffisait à produire la
chaîne de longueur ![]()
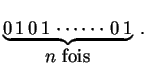
![]() est la quantité minimale d'information nécessaire pour produire
est la quantité minimale d'information nécessaire pour produire
![]() .
.
Remarque :
Bien que ceci n'ait pas la prétention d'être un cours de complexité, on
doit tout de même signaler que les définitions ci-dessus n'ont de sens
que si on restreint quelque peu la notion d'algorithme. Si on en reste aux
applications quelconques de ![]() dans
dans ![]() , on se heurte à des paradoxes
du type de celui de R. Berry :
, on se heurte à des paradoxes
du type de celui de R. Berry :
Pour engendrer une suite donnée de ![]() bits, l'algorithme brutal consiste
à les écrire tous les uns après les autres. Il correspond à
l'application identique
bits, l'algorithme brutal consiste
à les écrire tous les uns après les autres. Il correspond à
l'application identique ![]() de
de ![]() dans lui-même. Relativement à cet
algorithme la complexité de toute suite de
dans lui-même. Relativement à cet
algorithme la complexité de toute suite de ![]() bits est
bits est ![]() . Donc la
complexité de toute suite est majorée par sa longueur :
. Donc la
complexité de toute suite est majorée par sa longueur :
Dire qu'une suite est aléatoire, c'est dire qu'on ne peut pas faire mieux que l'algorithme brutal pour l'engendrer.
D'après la proposition suivante, la plupart des suites sont aléatoires.
Démonstration :Parmi les inputs susceptibles d'engendrer les suites de longueur
Concrètement, parmi toutes les suites de longueur ![]() , une proportion de
, une proportion de
![]() d'entre elles seulement sont de complexité
d'entre elles seulement sont de complexité ![]() .
.
Il devrait donc être facile de trouver des suites aléatoires puisque la plupart d'entre elles le sont. Paradoxement, le problème de démontrer qu'une suite particulière est aléatoire est indécidable en général.