Section : Données bidimensionnelles
Précédent : Régression linéaire simple
Suivant : Rapport de cotes

Régressions multiples

Le principe de la régression au sens des moindres carrés, tel qu'il a été décrit au paragraphe précédent, est très général. Etant donné un caractère $y$ "à expliquer" et des caractères $x^{(1)},\ldots,x^{(k)}$ "explicatifs", mesurés sur une même population de taille $n$, on cherche à isoler dans une famille de fonctions à plusieurs paramètres, une fonction $f$ qui "explique" $y$ par la relation :

$$y=f(x^{(1)},\ldots,x^{(k)})\;.$$

Comme critère de choix, on minimise sur toutes les fonctions de la famille l'erreur quadratique définie par :

$$EQ(f) = \frac{1}{n} \sum_{i=1}^n (y_i-f(x^{(1)}_i,\ldots,x^{(k)}_i))^2\;.$$

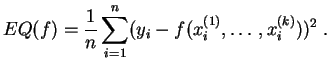
Dans certains cas classiques, on sait résoudre explicitement ce problème de minimisation, et la solution est implémentée dans les environnements de calculs statistiques. C'est le cas pour les exemples que nous donnons ci-dessous. Quand une résolution explicite est impossible, on a recours à des algorithmes de minimisation, comme l'algorithme du gradient.

Régression linéaire multiple.

C'est la généralisation directe de la régression linéaire simple du paragraphe précédent. Les fonctions $f$ sont affines :

$$f(x^{(1)},\ldots,x^{(k)}) = a_0 + a_1x^{(1)} + \cdots + a_kx^{(k)}\;.$$

L'erreur quadratique à minimiser est une fonction des $k+1$ paramètres inconnus $a_0,a_1,\ldots,a_k$.

$$EQ(a_0,\ldots,a_k) = \frac{1}{n} \sum_{i=1}^n (y_i- (a_0 + a_1x^{(1)}_i + \cdots + a_kx^{(k)}_i))^2\;.$$

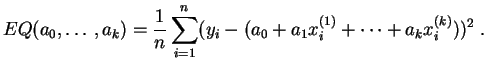
On peut toujours faire passer un hyperplan par $k$ points dans un espace de dimension $k+1$. Si la taille $n$ de la population est inférieure ou égale à $k$, l'erreur quadratique minimale est donc 0. En pratique, la régression ne pourra être significative que si $n$ est beaucoup plus grand que $k$.

Régression polynomiale simple.

On peut la voir comme une autre généralisation de la régression linéaire simple, ou comme un cas particulier de Régression linéaire multiple. Un seul caractère, $x$, est explicatif. Les fonctions $f$ sont les polynômes de degré $k$.

$$f(x) = a_0 + a_1x + \cdots + a_kx^k\;.$$

On peut considérer que les caractères $x,\ldots,x^k$ sont explicatifs pour se ramener au cas précédent. Les familles des polynômes de degrés successifs sont emboîtées. Pour un même ensemble de données, l'erreur quadratique diminuera donc si on augmente $k$, pour s'annuler quand $k$ dépasse $n$. Mais si $k$ est trop grand, la régression ne sera pas significative. En pratique, il est rare qu'une régression polynomiale aille au-delà du degré 3.

Régression polynomiale multiple.

Quand plusieurs caractères sont explicatifs, on peut encore effectuer une régression sur une famille de polynômes en les différents caractères, de degré fixé. Les termes faisant intervenir des produits du type $x^{(h)}x^{(h')}$ seront interprétés comme des termes d'interaction entre les caractères explicatifs. En pratique, on se limite à des polynômes de degré 1 ou 2. Voici pour deux caractères explicatifs $x^{(1)}$ et $x^{(2)}$, les modèles les plus fréquemment utilisés.

$\bullet$

Modèle d'ordre 1, sans interaction :

$$y=a_0+a_1x^{(1)}+a_2x^{(2)}\;.$$

$\bullet$

Modèle d'ordre 2, sans interaction :

$$y=a_0+a_1x^{(1)}+a_2x^{(2)}+a_3 (x^{(1)})^2 + a_4 (x^{(2)})^2\;.$$

$\bullet$

Modèle d'ordre 1, avec interaction :

$$y=a_0+a_1x^{(1)}+a_2x^{(2)}+a_3 x^{(1)}x^{(2)}\;.$$

$\bullet$

Modèle d'ordre 2, avec interaction :

$$y=a_0+a_1x^{(1)}+a_2x^{(2)}+a_3 (x^{(1)})^2 + a_4 (x^{(2)})^2 +a_5 x^{(1)}x^{(2)}\;.$$

Section : Données bidimensionnelles
Précédent : Régression linéaire simple
Suivant : Rapport de cotes