Ce paragraphe traite uniquement du cas de deux
caractères
binaires,
indicateurs de deux évènements différents dont on souhaite
étudier la dépendance. C'est un cas que l'on rencontre en médecine,
chaque fois qu'est posé le problème d'une détection
thérapeutique. Appelons ![]() (pour maladie) le premier évènement,
et
(pour maladie) le premier évènement,
et ![]() (pour symptôme) le second. Le symptôme peut être un taux
élevé d'une certaine substance ou la réaction positive à un
test
de dépistage, comme un alcootest. Sur chaque
individu
d'une
population
de taille
(pour symptôme) le second. Le symptôme peut être un taux
élevé d'une certaine substance ou la réaction positive à un
test
de dépistage, comme un alcootest. Sur chaque
individu
d'une
population
de taille ![]() , on a observé la présence ou l'absence de
la maladie et du symptôme. On dispose donc des 4
résultats suivants.
, on a observé la présence ou l'absence de
la maladie et du symptôme. On dispose donc des 4
résultats suivants.
Le problème est d'extraire de ces
données
de quoi étayer un diagnostic :
avec quelle certitude peut-on annoncer à un
individu
qu'il est malade
si on a constaté le symptôme sur lui ? En d'autres termes, peut-on
donner une valeur à la
probabilité conditionnelle
qu'un
individu
soit malade
sachant qu'il a le symptôme. Cette
probabilité
théorique, notée
![]() s'appelle la
valeur prédictive positive
du symptôme.
On peut la relier à d'autres quantités par la formule de Bayes :
s'appelle la
valeur prédictive positive
du symptôme.
On peut la relier à d'autres quantités par la formule de Bayes :
![$\displaystyle P[M\,\vert\,S] = \frac{P[S\,\vert\,M]P[M]}{P[S\,\vert\,M]P[M]+P[S\,\vert\,\overline{M}]
P[\overline{M}]}\;.
$](img276.gif)
La
probabilité
![]() , qui représente la proportion de malades dans
la
population
est souvent très faible et
difficile à estimer de façon fiable. Une des raisons
est que la maladie n'est détectée que parmi les personnes qui se
présentent à une consultation, et qui par là même ne sont pas
représentatives de l'ensemble de la
population.
Dans l'exemple de
l'alcootest il est même impossible de définir la proportion
des individus qui ont trop bu, car elle dépend de l'heure de la journée,
du lieu, etc... Les
probabilités conditionnelles
du symptôme
sachant la maladie sont en général les seules accessibles.
, qui représente la proportion de malades dans
la
population
est souvent très faible et
difficile à estimer de façon fiable. Une des raisons
est que la maladie n'est détectée que parmi les personnes qui se
présentent à une consultation, et qui par là même ne sont pas
représentatives de l'ensemble de la
population.
Dans l'exemple de
l'alcootest il est même impossible de définir la proportion
des individus qui ont trop bu, car elle dépend de l'heure de la journée,
du lieu, etc... Les
probabilités conditionnelles
du symptôme
sachant la maladie sont en général les seules accessibles.
Dans un cas idéal, ces deux quantités devraient valoir 1. Un alcootest parfait devrait être positif sur tout individu ayant trop bu, et ne jamais accuser à tort un conducteur sobre. En pratique, la sensibilité et la spécificité sont souvent élevées, avec des différences importantes selon les tests. Pour une maladie sans traitement connu, il est plus grave d'alarmer à tort une personne non atteinte, que de ne pas détecter un patient atteint. On choisira donc des tests à très forte spécificité, quitte à ce que leur sensibilité soit moins bonne. A l'inverse, pour une maladie potentiellement grave mais facilement soignable, on utilisera des tests à forte sensibilité.
Une forte
sensibilité
et une forte
spécificité
ne
garantissent pas que la
valeur prédictive positive
soit bonne, si la
proportion de malades est faible. Supposons par exemple
![]() et
et
![]() .
D'après la formule de Bayes, la
valeur prédictive positive
vaut :
.
D'après la formule de Bayes, la
valeur prédictive positive
vaut :
![$\displaystyle P[M\,\vert\,S] = \frac{0.9\;0.01}{0.9\;0.01 + 0.1\;0.99} = \frac{1}{12}\;.
$](img282.gif)
Concrètement, sur 12 personnes présentant le symptôme, 11
ne sont pas malades. Si on s'arrête à ce chiffre, il semble
inquiétant. Mais si on calcule de même
![]() , on
trouve 1/892. La proportion de malades parmi les individus qui présentent
le symptôme est tout de même beaucoup plus forte que parmi les autres.
On dira que le symptôme est en faveur de la maladie. La question se pose donc
d'évaluer l'efficacité du symptôme dans la détection de la maladie,
par un nombre qui ne dépende pas de
, on
trouve 1/892. La proportion de malades parmi les individus qui présentent
le symptôme est tout de même beaucoup plus forte que parmi les autres.
On dira que le symptôme est en faveur de la maladie. La question se pose donc
d'évaluer l'efficacité du symptôme dans la détection de la maladie,
par un nombre qui ne dépende pas de ![]() .
.
On utilise pour cela le
rapport de cotes
(odds-ratio en anglais). La
cote (au sens des parieurs) d'un évènement est le rapport de
la
probabilité
de l'évènement à celle de son complémentaire.
La cote de la maladie peut se calculer parmi les individus ayant le
symptôme (
![]() ) et parmi ceux qui ne l'ont
pas (
) et parmi ceux qui ne l'ont
pas (
![]() ). Le
rapport de cotes
théorique est le quotient de ces deux quantités.
). Le
rapport de cotes
théorique est le quotient de ces deux quantités.
![$\displaystyle RC = \frac{P[M\,\vert\,S]/P[\overline{M}\,\vert\,S]}{
P[M\,\vert\...
...overline{M}\cap\overline{S}]}{
P[\overline{M}\cap S]\,P[M\cap\overline{S}]}\;.
$](img288.gif)
Le rapport de cotes vaut 1 si la maladie et le symptôme sont indépendants, il est supérieur à 1 si le symptôme est en faveur de la maladie. Quand des observations ont été menées sur un échantillon, on peut approcher les probabilités théoriques par des fréquences expérimentales. Ceci conduit à la définition du rapport de cotes empirique.
Quand le dénominateur est nul, on convient de remplacer la définition
de
![]() par :
par :
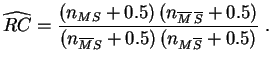
Exemple :
Supposons que pour un
échantillon
de ![]() individus, la
répartition soit la suivante :
individus, la
répartition soit la suivante :
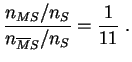
Il y a 1 malade pour 11 non malades parmi les individus ayant le symptôme. Pour ceux qui n'ont pas le symptôme, la cote est :
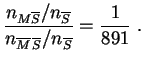
Il y a 1 malade pour 891 non malades parmi les individus n'ayant pas le symptôme. Le rapport de cotes empirique vaut :
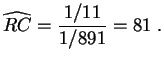
Le symptôme est donc bien en faveur de la maladie.