Section : Distribution empirique
Précédent : Distribution empirique
Suivant : Quantiles

Représentations graphiques

La distribution empirique associée à un échantillon est la distribution de probabilité sur l'ensemble des modalités qui affecte chaque observation du poids 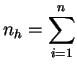$ 1/n$.

Définition 2.1   Soit $ (x_1,\ldots,x_n)$ un échantillon, $ c_1,\ldots,c_k$ les valeurs distinctes prises par les $ x_i$ et pour $ h=1,\ldots,k$ :

$\displaystyle n_h = \sum_{i=1}^n$   1$\displaystyle _{c_h}(x_i)\;, $

l'effectif de la valeur $ c_h$. La distribution empirique de l'échantillon est la loi de probabilité $ \widehat{P}$ sur l'ensemble $ \{c_1,\ldots,c_k\}$, telle que :

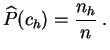
$\displaystyle \widehat{P}(c_h) = \frac{n_h}{n}\;. $

La moyenne, la variance et l'écart-type peuvent être vus comme des caractéristiques de la distribution empirique. La moyenne de l'échantillon est l'espérance de sa distribution empirique. Pour un caractère discret, ou continu regroupé en classes, la valeur modale, ou mode de la distribution empirique est la valeur (ou la classe) qui a la fréquence la plus élevée. Une distribution empirique est dite unimodale si cette fréquence est significativement plus grande que les autres. Elle peut être bimodale ou multimodale dans d'autres cas.

Pour étudier une distribution empirique, la première étape consiste à trier les données par ordre croissant, à savoir écrire ses statistiques d'ordre .

Définition 2.2   Soit $ (x_1,\ldots,x_n)$ un échantillon numérique. On appelle statistiques d'ordre de l'échantillon, les valeurs $ x_{(1)},\ldots,x_{(n)}$ égales aux $ x_i$ rangées par ordre croissant.

$\displaystyle x_{(1)} = \min_{i=1,\ldots,n}\{x_i\}\leq x_{(2)}\leq\cdots\leq x_{(n)} = \max_{i=1,\ldots,n}\{x_i\}\;. $

Voici par exemple un échantillon de taille 10 et ses 10 statistiques d'ordre.

5.7
3.2
8.4
4.1
6.9
5.3
1.7
3.2
2.5
7.4
1.7
2.5
3.2
3.2
4.1
5.3
5.7
6.9
7.4
8.4
La fonction de répartition empirique est la fonction de répartition de la distribution empirique.

Définition 2.3   La fonction de répartition empirique est la fonction, notée $ \widehat{F}$, de $ \mathbb{R}$ dans $ [0,1]$, qui vaut :

\begin{displaymath} \widehat{F}(x) = \left\{ \begin{array}{lcl} 0 &\mbox{pour}& ... ...&\vdots&\\ 1&\mbox{pour}&x\geq x_{(n)}\;. \end{array}\right. \end{displaymath}

En d'autres termes, $ \widehat{F}(x)$ est la proportion d'éléments de l' échantillon qui sont inférieurs ou égaux à $ x$. Représenter la fonction de répartition empirique (en général on trace seulement les points de coordonnées $ (x_{(i)},i/n))$, donne une idée de la distribution empirique.

Dans le cas où l'échantillon est discret (le nombre de valeurs différentes $ k$ est faible devant la taille de l'échantillon $ n$), on représentera la distribution empirique par un diagramme en bâtons . Il consiste à représenter les valeurs différentes $ c_1,\ldots,c_k$ en abscisse, avec au-dessus de chacune une barre verticale de longueur égale à sa fréquence expérimentale $ f(c_h)$. Dans le cas où le nombre de valeurs différentes est très faible (inférieur à 10), et surtout pour des échantillons qualitatifs, on utilise aussi des représentations en camembert (pie-chart), ou en barre. Elles consistent à diviser un disque ou un rectangle proportionnellement aux différentes fréquences.

La représentation correspondant au diagramme en bâtons pour un échantillon considéré comme continu (lorsque presque toutes les valeurs sont différentes), est l'histogramme. Il suppose que l'on a choisi un nombre de classes $ k$ et un intervalle de représentation $ [a_0,a_k]$, que l'on a découpé en $ k$ intervalles $ [a_0,a_1], ]a_1,a_2],\ldots,]a_{k-1}, a_k]$. On remplace alors la distribution empirique par une nouvelle loi de probabilité, qui pour tout $ h=1,\ldots,k$, charge l'intervalle $ ]a_{h-1},a_h]$ avec sa fréquence expérimentale $ \widehat{P}(]a_{h-1},a_h])$ :

$\displaystyle \widehat{P}(]a_{h-1},a_h]) = \frac{1}{n} \sum_{i=1}^n$   1$\displaystyle _{]a_{h-1},a_h]}(x_i)\;. $

Tracer un histogramme consiste à représenter les classes en abscisses, avec au dessus de la $ h$-ième un rectangle de hauteur $ f_h/(a_{h-1}-a_h)$, donc de surface égale à $ f_h$. Cette représentation est celle d'une densité de probabilité, constante sur chacune des classes. Représenter un histogramme implique un certain a priori sur les données. On décide en effet que la fréquence de chacune des classes est bien sa fréquence empirique dans l'échantillon, mais que la distribution des données à l'intérieur de chaque intervalle est aléatoire, de loi uniforme sur cet intervalle.


Section : Distribution empirique
Précédent : Distribution empirique
Suivant : Quantiles