Section : Hypothèses alternatives
Précédent : Test du rapport de vraisemblance

Fonction puissance

La notion de puissance a été définie jusqu'ici pour une alternative simple. Dans le cadre paramétrique, si l'hypothèse $ {\cal H}_1$ est composée, on utilisera plutôt la fonction puissance. On dispose d'un échantillon $ (X_1,\ldots,X_n)$ de la loi $ P_\theta$ dépendant du paramètre $ \theta$. On suppose que pour une certaine hypothèse $ {\cal H}_0$, une règle de rejet a été définie.

Définition 4.7   On appelle fonction puissance la fonction qui à une valeur $ \theta$ du paramètre associe :

$\displaystyle \pi(\theta) = \mathbb{P}_\theta[\,$Rejet de $\displaystyle {\cal H}_0\,]\;, $

où $ \mathbb{P}_\theta$ désigne la loi de l'échantillon, quand la valeur du paramètre est $ \theta$.

Si l'hypothèse $ {\cal H}_0$ est simple, du type $ \theta=\theta_0$, alors la valeur de la fonction puissance pour $ \theta_0$ est le seuil du test : $ \pi(\theta_0) = \alpha$.


Considérons par exemple un échantillon de la loi exponentielle de paramètre $ \lambda$. La moyenne empirique $ \overline{X}$ suit la loi gamma $ {\cal G}(n,n\lambda)$. Considérons l'hypothèse simple $ {\cal H}_0\,:\,\lambda=1$, et les trois tests (bilatéral, unilatéral à droite et à gauche) définis par les règles de décision :

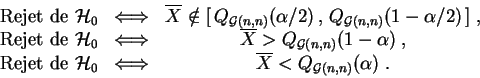
\begin{displaymath}\begin{array}{ccc} \mbox{Rejet de }{\cal H}_0&\Longleftrighta... ...tarrow& \overline{X} < Q_{{\cal G}(n,n)}(\alpha)\;. \end{array}\end{displaymath}

Si la valeur du paramètre est $ \lambda$, on calcule les probabilités de rejet de $ {\cal H}_0$, à l'aide de la fonction de répartition de la loi gamma $ {\cal G}(n,n\lambda)$. Comme exemple numérique, nous fixons $ n=$10 et $ \alpha=$0.05. Voici quelques valeurs particulières pour les 3 fonctions puissance

$ \pi_1(\lambda)$, $ \pi_2(\lambda)$ et $ \pi_3(\lambda)$.

$ \lambda$
0.7
0.8
0.9
1
1.1
1.2
1.3
$ \pi_1(\lambda)$
0.248
0.132
0.072
0.050
0.053
0.072
0.102
$ \pi_2(\lambda)$
0.341
0.197
0.103
0.050
0.023
0.010
0.004
$ \pi_3(\lambda)$
0.006
0.014
0.028
0.050
0.082
0.124
0.175

Pour le test bilatéral, la fonction puissance admet un minimum au point $ \lambda=1$. Pour les tests unilatéraux, la puissance est monotone, et elle est inférieure au seuil du test pour certaines valeurs de $ \lambda$.

Définition 4.8   On dit qu'un test de seuil $ \alpha$ pour une hypothèse simple $ {\cal H}_0\,:\,\theta=\theta_0$ est biaisé si la fonction puissance prend des valeurs inférieures à $ \alpha$ pour certaines valeurs de $ \theta$.

Pour les tests où l'alternative est simple, le théorème de Neyman-Pearson affirme que le test du rapport de vraisemblance est le plus puissant pour un seuil donné. Un tel test est dit uniformément le plus puissant (UPP, ou UMP en anglais). Pour des hypothèses composées, il n'existe pas en général de test UPP. Sous des hypothèses raisonnables, on démontre qu'il existe toujours un test qui soit UPP parmi les tests non biaisés.


Section : Hypothèses alternatives
Précédent : Test du rapport de vraisemblance