Implémentation en C d’Estimateurs non paramétriques de quantiles conditionnels

– Application au tracé de courbes de référence -

Ali Gannoun^1,2, Stéphane Girard³, Christiane Guinot⁴ et Jérôme Saracco¹

¹Laboratoire de Probabilités et Statistique, CC 051, Université Montpellier II,

Place Eugène Bataillon, 34095 Montpellier Cedex 5

e-mail : {gannoun,saracco}@stat.math.univ-montp2.fr

²Statistical Genetics and Bioinformatics Unit, National Human Genome Center,

Howard University, Washington D.C. 20059, USA

e-mail : agannoun@howard.edu

³ CE.R.I.E.S,

20, Rue Victor Noir, 92 521 Neuilly sur Seine Cedex

e-mail : christiane.guinot@ceries-lab.com

⁴SMS/LMC, Université Grenoble I,

38041 Grenoble Cedex 9

e-mail : Stephane.Girard@imag.fr

Résumé : Nous présentons ici trois méthodes d’estimation non paramétrique des quantiles conditionnels : une méthode d'estimation par noyau (cas unidimensionnel et multidimensionnel), la méthode de la constante locale et une méthode d'estimation par noyau produit. Nous décrivons ensuite ici l’implémentation informatique en C de ces méthodes. Une interface avec les logiciels SAS, Splus et Gnuplot est donnée afin d’appliquer les résultats au tracé de courbes de référence. Enfin, nous terminons en donnant une illustration. sur des données réelles concernant des propriétés biophysiques de la peau de femmes japonaises.

Mots-clés : Courbes de référence, quantiles conditionnels, méthode d'estimation par noyau, méthode de la constante locale, méthode d'estimation par noyau produit.

1. Introduction aux quantiles conditionnels et aux courbes de référence

Nous faisons dans cette partie une brève présentation de la notion de quantile conditionnel et de celle de courbes de référence. Pour avoir plus de détails et des références bibliographiques, nous renvoyons le lecteur à l’article Gannoun et al. (2002).

1.1. Quantiles conditionnels

Considérons deux variables quantitatives continues : une variable Y, appelée variable d’intérêt, et une variable X, appelée covariable. Soit.

Le quantile conditionnel d'ordre α de la variable Y sachant que X=x est défini de la manière suivante :

où F(.|x) désigne la fonction de répartition conditionnelle de Y sachant que X=x.

Une caractérisation alternative de quantile conditionnel est obtenue sous forme d'un problème d'optimisation (P) :

où est la fonction définie par :

Plusieurs approches ont été développées pour l'estimation des quantiles conditionnels. L'approche paramétrique peut parfois être mal adaptée à la réalité des données en particulier biologiques. Une approche non paramétrique du problème a alors été développée afin de pallier les problèmes d'hypothèses et de modélisation paramétriques. De nombreux travaux récents ont été menés pour l'estimation non paramétrique des quantiles conditionnels aussi bien dans un cadre théorique que sur le plan des applications. Ces méthodes ne nécessitent pas d'hypothèse sur la nature de la distribution.

Nous présentons brièvement ici trois méthodes non paramétriques d'estimation des quantiles conditionnels et leur implémentation en C :

· une méthode d'estimation par noyau,

· la méthode de la constante locale (« local constant kernel estimation »),

· une méthode d'estimation par noyau produit (« double kernel estimation »).

1.2. Courbes de référence

De nombreuses expérimentations, en particulier dans les domaines biomédical, biométrique et industriel, sont conduites pour établir des intervalles de valeurs qui sont prises « normalement » par une variable d'intérêt Y dans une population cible. Ici, le terme « normalement » fait référence aux valeurs que l'on est susceptible d'observer avec une probabilité donnée, dans des conditions normales et pour des individus types présumés en bonne santé ou sans défaut (les sujets de référence). Ces intervalles sont souvent appelés intervalles de référence et les valeurs correspondantes sont appelées valeurs de référence. Par exemple, on peut s'intéresser à un intervalle excluant les 5% d'observations les plus grandes et les 5% d'observations les plus petites. Ainsi, la construction d'intervalles de référence repose naturellement sur le calcul de quantiles.

Par ailleurs, il arrive régulièrement que, sur la population cible, l'on dispose simultanément, avec la variable d'intérêt Y, d'une information complémentaire sous la forme d'une covariable X. Pour une valeur donnée x de X, on peut construire un intervalle de référence. Lorsque x varie, on obtient alors des courbes de référence. Dans ce cadre-là, il est nécessaire de travailler avec les quantiles conditionnels de Y sachant X. Le tracé de courbes de référence sur le nuage des valeurs prises par le couple (X, Y) pour les sujets de référence donne un résumé graphique très utile et interprétable. Ainsi, un individu i représenté par le point pourra être comparé à la population de référence. En d'autres termes, cet individu sera suspectée d’être « hors normes » si ce point se situe en dessous de la courbe de référence inférieure ou au dessus de la courbe de référence supérieure.

Plus précisément, pour une valeur x donnée et α>1/2, l'intervalle de référence contenant 100(2α-1)% des sujets de référence est ensuite défini par : I_α(x). Les courbes de référence sont alors les ensembles de points et lorsque x varie. Soit un estimateur de à partir de l'échantillon de n réalisations indépendantes du couple (X, Y). L'estimateur correspondant de I_α(x) est défini par : I_n,α(x) . En pratique, pour obtenir les courbes de référence à 90%, α est choisi égal à 0.95.

En pratique pour estimer les courbes de référence, on évalue les quantiles conditionnels d’ordres α et 1-α sur un ensemble fini de T points . On obtient donc les ensembles des points et . Pour la représentation graphique des courbes de référence, une approche basique consiste à réaliser une interpolation linéaire entre ces différents points. Cependant les courbes obtenues avec cette approche présentent un aspect visuel non ``lisse''. Ainsi, pour pallier ce défaut, il est aussi possible d’opter pour un lissage par la méthode du noyau (de type Nadaraya-Watson) de ces points, le noyau choisi étant le noyau normal et la fenêtre utilisée étant obtenue par validation croisée.

La suite de cet article est organisée de la façon suivante. Nous présentons rapidement dans la partie 2 les estimateurs non paramétriques des quantiles conditionnels mentionnés ci-dessus. Nous précisons également le choix des différents paramètres de lissage intervenant dans ces estimateurs. La partie 3 est consacrée à la description de l’implémentation en C de ces estimateurs. Dans la partie 4, nous décrivons l’interface avec d’autres logiciels (Splus, SAS, Gnuplot) dans le cadre de l’application au tracé de courbes de référence. La partie 5 montre une mise en oeuvre à une étude visant à établir des courbes de référence, en fonction de l'âge, de propriétés biophysiques de la peau de femmes japonaises.

2. Présentation rapide de méthodes non paramétriques d’estimation des quantiles conditionnels

Nous décrivons ici les trois méthodes d'estimation non paramétrique des quantiles conditionnels dans le cas où X est unidimensionnelle, ainsi qu’une généralisation de la première méthode au cas multidimensionnel. Les premier et troisième estimateurs reposent sur l’estimation de la fonction de répartition conditionnelle puis sur son inversion pour obtenir une estimation du quantile conditionnel, le second estimateur est quant à lui un estimateur direct du quantile conditionnel.

2.1. Méthode 1 : méthode d'estimation par noyau

Définissons tout d'abord un estimateur non paramétrique de la fonction de répartition conditionnelle de Y sachant X=x, pour :

.

La fonction K, appelée noyau, est généralement une densité de probabilité. Le paramètre h_n permet de contrôler le lissage appliqué aux données. Son choix en pratique est discuté dans le paragraphe 2.5.

Il est alors naturel d'estimer le quantile conditionnel par de la manière suivante :

.

2.2. Méthode 2 : méthode de la constante locale

Une approche linéaire locale a été développée pour résoudre le problème (P). Le quantile inconnu est approché par une fonction linéaire, pour z dans un voisinage de x :

la notation désignant la dérivée de . Localement, estimer est alors équivalent à estimer le coefficient a, et estimer revient à estimer b. Ainsi, on peut définir des estimateurs de et en minimisant par rapport à a et b la quantité

où et K désignent la fenêtre et le noyau mentionnés précédemment. Si b=0, on définit la méthode dite de la constante locale, et on obtient, pour , l'estimateur suivant :

Cette méthode directe d'estimation présente en particulier l'avantage d'un bon comportement face aux effets de bords.

2.3. Méthode 3 : méthode d'estimation par noyau produit

Une version plus « lisse » de l'estimateur de la fonction de répartition conditionnelle définie au paragraphe 2.1 peut être introduite en remplaçant la fonction indicatrice par une nouvelle densité symétrique ω. 'estimateur correspondant, appelé estimateur par noyau produit est défini comme suit pour  :

où est la fonction de répartition associée à . Cet estimateur peut également être vu comme l'intégrale de l'estimateur à noyau de la densité conditionnelle.

Il en découle naturellement un estimateur du quantile conditionnel défini par

Cette approche est attractive mais nécessite le choix de deux paramètres de lissage et . Il apparaît en pratique que cet estimateur est extrêmement sensible au choix de ces deux paramètres. Une méthode empirique pour choisir et a été proposée par Yu et Jones (1998), et sera décrite dans le paragraphe 2.5.

2.4. Cas multidimensionnel : méthode d'estimation par noyau

Le principe d’estimation est identique à celui décrit dans le paragraphe 2.1. La fonction de répartition conditionnelle est estimée non paramétriquement par la méthode du noyau. Formellement, cet estimateur a exactement la même écriture que dans le cas unidimensionnel du paragraphe 2.1, mais le noyau utilisé est une densité de probabilité multidimensionnelle. Par souci de simplicité, nous avons utilisé une densité multidimensionnelle définie par un produit de densités unidimensionnelles identiques. De même, le paramètre de lissage est choisi identique selon toutes les coordonnées. Le quantile conditionnel est alors estimé par inversion de l’estimateur de la fonction de répartition conditionelle.

2.5. Choix des noyaux et des paramètres de lissage

Nous indiquons dans ce paragraphe les choix de noyaux et de fenêtres qui sont utilisés dans l’implémentation en C de ces différentes méthodes.

Choix des noyaux : La qualité des estimateurs n'étant pas très affectée par le choix des noyaux, nous utilisons les noyaux K et suivants :

- le noyau normal : pour ,

- le noyau uniforme : pour .

Choix des paramètres de lissage : Le choix de la fenêtre est quant à lui crucial. La qualité des estimateurs non paramétriques basés sur les noyaux y est étroitement liée. Une importante littérature est consacrée à ce sujet, et en particulier aux méthodes de sélection automatique par minimisation d'un critère. La méthode de validation croisée entre dans ce cadre. Nous avons retenu les choix suivants pour les différentes fenêtres intervenant dans chacun des estimateurs.

- Pour l'estimateur , une approche dérivée du critère de validation croisée est utilisée (voir Yao (1999)) :

où est l'estimateur de $F(.|x)$ défini au paragraphe 2.1 mais calculé à partir de l'échantillon privé de la t-ème observation.

- Pour l'estimateur , Yu et Jones (1998) proposent la règle empirique suivante :

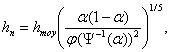
où est la fenêtre obtenue par validation croisée dans le cadre de la régression à noyau de Y sur X. Cette règle repose sur l'hypothèse de normalité de la loi conditionnelle de Y sachant X. Les fonctions φ et Ψ sont respectivement la densité et la fonction de répartition de la loi normale centrée réduite. Dans les cas où α=0,05 et α=0,95, la table 1 de Yu et Jones (1998) donne .

- Pour l'estimateur , le choix de deux fenêtres est nécessaire. Nous utilisons encore les méthodes proposées par Yu et Jones (1998). Le choix de la première fenêtre est identique à celui de la fenêtre décrit par la formule précédente. Pour la sélection de la fenêtre , la règle suivante a été adoptée :

où est l'évaluation de l'expression (\ref{deux}) lorsque α=0,5.

L'utilisation de telles règles empiriques présente l'avantage d'une mise en oeuvre simple et rapide. Cependant cet avantage est acquis au prix d'une perte de généralité due à l'ajout d'une hypothèse de normalité.

2.6. Remarques

Les approches non paramétriques présentées ici sont robustes, et les courbes de référence sont ainsi déterminées sans détection préalable des points aberrants. Dans les études empiriques que nous avons réalisées (voir Gannoun et al. (2002)), il apparaît que deux des estimateurs non paramétriques fournissent des courbes de référence acceptables pour la presque totalité des variables étudiées. Cette analyse statistique peut ainsi être très utile pour la détermination de courbes de référence à partir de données d'une fiabilité médiocre. Le troisième estimateur (méthode d'estimation par noyau produit) pose encore quelques problèmes pratiques provenant du choix des fenêtres, d'autres règles doivent être étudiées. Deux possibilités peuvent être envisagées : une méthode de type validation croisée, ne nécessitant pas d'hypothèse sous-jacente mais numériquement coûteuse, ou le développement d'une règle empirique plus adaptée à la nature du bruit observé.

3. Implémentation en C

Deux programmes en C ont été développés : le premier « estimateurV2 » concerne le cas où la covariable X est unidimensionnelle et permet d’estimer les quantiles conditionnels avec les trois méthodes non paramétriques décrites précédemment ; le second « multiestimateur » permet de faire l’estimation non paramétrique (par noyau) des quantiles conditionnels lorsque la covariable est multidimensionnelle.

Ces deux programmes permettent d’estimer les quantiles conditionnels d’ordre α à partir des données sur une grille , la covariable et les points de la grille d’évaluation ayant même dimension. Dans les fichiers de données ou de grille, les individus sont en ligne et les séparateurs sont des espaces.

3.1. Cas unidimensionnel : programme « estimateurV2 »

Un fichier de paramètres (appelé ici « essai.par » ) doit tout d’abord être complété avant de lancer l’exécution des calculs de quantiles conditionnels.

Exemple de fichier « essai.par » (environnement Linux pour les répertoires) :

Methode_________________________________________: 1

Lissage_Quantiles_Conditionnels_(1=oui)_________: 1

Repertoire_Donnees______________________________: ../Donnees/

Repertoire_Resultats____________________________: ../Resultat/

Nom_Fichier_Donnees_____________________________: donnees

Ordre_Quantile_[1_100]__________________________: 95

Nombre_Essais_Calcul_Quantile___________________: 20

Nom_Fichier_Points_Evaluation_Quantile__________: grille.dat

Nombre_Essais_Recherche_H_Optimal_______________: 20

H_Optimal(aux_si_methode=3)__si_0_ci_dessus_____: 8

Les différents paramètres sont les suivants :

· Methode : 1, 2 ou 3 en fonction de la méthode de calcul désiré pour les quantiles conditionnels ;

· Lissage_Quantiles_Conditionnels_(1=oui) : 1 pour oui ou 0 pour non si l’utilisateur désire ou non une lissage par noyau des points , ceci donnera lieu à la création d’un fichier de sortie supplémentaire portant l’extension « .lis » ;

· Repertoire_Donnees : il s’agit d’indiquer ici l’adresse du répertoire dans lequel se trouve le fichier des données  ;

· Repertoire_Resultats : il s’agit d’indiquer ici l’adresse du répertoire dans lequel seront stockés les différents fichiers de résultats ;

· Nom_Fichier_Donnees : il s’agit données ici le nom du fichier des données, ce dernier doit avoir l’extension « .dat », extension qu’il ne faut pas préciser dans le fichier de paramètres ;

· Ordre_Quantile_[1_100] : il faut préciser ici l’ordre α du quantile conditionnel, attention le programme estime automatiquement les quantiles conditionnels d’ordres α et 1-α ;

· Nombre_Essais_Calcul_Quantile : il s’agit ici de préciser, pour les méthodes 1 et 3, le nombre désiré de pas dans l’inversion de la fonction de répartition conditionnelle afin d’obtenir une estimation du quantile conditionnel ;

· Nom_Fichier_Points_Evaluation_Quantile : il s’agit d’indiquer ici le nom du fichier contenant la grille sur laquelle vont être estimés les quantiles conditionnels, ce dernier n’a pas d’extension par défaut et doit se situer dans le même répertoire que celui du fichier des données  ;

· Nombre_Essais_Recherche_H_Optimal : il s’agit ici de préciser, pour les différentes méthodes, le nombre désiré d’essais dans la recherche automatique (selon les critères présentés précédemment) de la ou des fenêtres optimales, si l’utilisateur précise 0 (zéro), la ou les fenêtres optimales ne seront pas recherchées automatiquement mais les valeurs seront précisées par l’utilisateur à la ligne suivante du fichiers de paramètres ;

· H_Optimal(aux_si_methode=3)__si_0_ci_dessus : si l’utilisateur a décidé de ne faire une recherche automatique de la ou des fenêtres optimales, il doit préciser ici la ou les valeurs choisies « arbitrairement » : une fenêtre pour les méthodes 1 ou 2, ou deux fenêtres et pour la méthode 3.

Après avoir lancé les calculs à partir ce fichier de paramètres (taper par exemple la commande ./estimateurV2 essai.par dans l’environnement Linux), les calculs vont s’effectuer en une ou plusieurs étapes :

- Etape 1 : recherche (si nécessaire) de la ou des fenêtres optimales,

- Etape 2 : calcul des quantiles conditionnels d’ordres α et 1-α sur les points de la grille,

- Etape 3 : lissage éventuel des quantiles conditionnels.

A l’issu des ces tapes de calculs, plusieurs fichiers (3 s’il n’y a pas de lissage des quantiles conditionnels, ou 5 sinon) seront créés dans le répertoire des résultats. Avant de donner leur description ci-après, précisons que les noms de tous ces fichiers commencent par est1. (ou est2. ou est3.) en fonction de la méthode de calcul choisie, suivi du nom du fichier des données (ici donnees.). Par exemple, les fichiers disponibles sont :

· est1.donnees.CV : ce fichier contient (en ligne) les points concernant la recherche des fenêtres optimales par validation croisée (il s’agit de la recherche de pour l’estimateur 1, et de la recherche de pour les estimateurs 2 et3).

· est1.donnees.Qn5 : ce fichier contient (en ligne) les points .

· est1.donnees.Qn5.lis : ce fichier contient (en ligne) une version lissée par noyau du nuage des points précédents : .

· est1.donnees.Qn95 : ce fichier contient (en ligne) les points .

· est1.donnees.Qn95.lis : ce fichier contient (en ligne) une version lissée par noyau du nuage des points précédents :

A titre indicatif, le temps nécessaire au calcul et au lissage des quantiles conditionnels d’ordre 5% et 95% est de 2 minutes 30 secondes sur un Pentium III, 450 Mhz dans les conditions suivantes : n=200 points, grille de T=20 points, 20 itérations pour le calcul des quantiles conditionnels, 20 itérations pour la recherche du paramètre de lissage optimal.

3.2. Cas multidimensionnel : programme « multiestimateur »

Ici aussi, un fichier de paramètres (appelé ici « essaimulti.par » ) doit tout d’abord être complété avant de lancer l’exécution des calculs de quantiles conditionnels.

Fichier « essaimulti.par » (environnement Linux pour les répertoires) :

Repertoire_Donnees______________________________: ../Donnees/

Repertoire_Resultats____________________________: ../Resultat/

Nom_Fichier_Donnees_____________________________: donneesmulti

Dimension_Covariable____________________________: 3

Ordre_Quantile_[1_100]__________________________: 95

Nombre_Essais_Calcul_Quantile___________________: 20

Nom_Fichier_Points_Evaluation_Quantile__________: grille3D.dat

Nombre_Essais_Recherche_H_Optimal_______________: 20

H_Optimal(aux_si_methode=3)__si_0_ci_dessus_____: 8

La plupart des paramètres sont identiques à ceux nécessaires dans le cadre unidimensionnel. Les seuls changements notables sont les suivants :

· il n’y a plus de choix pour la méthode d’estimation (seule la méthode d’estimation par noyau est disponible),

· il faut préciser la dimension de la covariable (ligne Dimension_Covariable),

· il n’y a pas possibilité de faire du lissage a posteriori des quantiles conditionnels estimés (on lisserait une hyper-surface et non plus une courbe, cela reste techniquement possible mais cela nécessiterait un grand nombre de points sur la grille multidimensionnelle).

Rappelons que le choix de l’ordre α du quantile conditionnel entraîne aussi automatiquement le calcul du quantile conditionnel d’ordre 1-α.

Après avoir lancé les calculs à partir ce fichier de paramètres (taper par exemple la commande ./multiestimateur essaimulti.par dans l’environnement Linux), les calculs vont s’effectuer en une ou plusieurs étapes :

- Etape 1 : recherche (si nécessaire) de la fenêtre optimale,

- Etape 2 : calcul des quantiles conditionnels d’ordres α et 1-α sur les points de la grille.

A l’issu des ces tapes de calculs, trois fichiers sont créés dans le répertoire des résultats. Les noms de ces fichiers commencent par est1., suivi du nom du fichier des données (ici donneesmulti.). On retrouve ainsi les fichiers : est1.donneesmulti.CV, est1.donneesmulti.Qn5 et est1.donneesmulti.Qn95.

Le temps de calcul nécessaire est proportionnel au nombre de covariables. Pour une seule covariable, le temps est de 2 minutes 30 dans les conditions décrites au paragraphe 3.1.

4. Interface avec d’autres logiciels : application au tracé de courbes de référence

Il s’agit ici de fournir des petits programmes (en Splus, SAS et Gnuplot) permettant de représenter le nuage des points et de tracer les courbes de référence correspondantes dans le cas unidimensionnel, à partir du fichier des données (par exemple : donnees.dat) ainsi que des fichiers de sorties obtenus par les programmes C précédents (par exemple avec la méthode d’estimation 1 et en ayant demandé un lissage a posteriori des quantiles conditionnels : est1.donnees.CV, est1.donnees.Qn5, est1.donnees.Qn5.lis, est1.donnees.Qn95 et est1.donnees.Qn95.lis). On supposera que ces fichiers sont contenus dans le répertoire « C:\Temp » dans l’environnement Windows, en ce qui concerne les interfaces Splus et SAS.

4.1. Interface avec Splus

# Recuperation des donnees et des resultats dans des objets Splus

#================================================================

donnees_matrix(scan("c:\\Temp\\donnees.dat"),ncol=2,byrow=T)

quant5_matrix(scan("c:\\Temp\\est1.donnees.Qn5"),ncol=2,byrow=T)

quant95_matrix(scan("c:\\Temp\\est1.donnees.Qn95"),ncol=2,byrow=T)

quant5lis_matrix(scan("c:\\Temp\\est1.donnees.Qn5.lis"),ncol=2,byrow=T)

quant95lis_matrix(scan("c:\\Temp\\est1.donnees.Qn95.lis"),ncol=2,byrow=T)

CV_matrix(scan("c:\\Temp\\est1.donnees.CV"),ncol=2,byrow=T)

# Fonction permettant de tracer le nuage de points et les courbes de reference

#=============================================================================

graphCourbesRef_function(donnees,quant5, quant95){

xmin_min(donnees[,1],quant5[,1])

xmax_max(donnees[,1],quant5[,1])

ymin_min(donnees[,2],quant5[,2],quant95[,2],quant5lis[,2],quant95lis[,2])

ymax_max(donnees[,2],quant5[,2],quant95[,2],quant5lis[,2],quant95lis[,2])

plot(donnees,pch=3,xlim=c(xmin,xmax),ylim=c(ymin,ymax),xlab="x",ylab="y")

par(new=T)

plot(quant5,type="l",lty=1,xlim=c(xmin,xmax),ylim=c(ymin,ymax),xlab="x",ylab="y")

par(new=T)

plot(quant95,type="l",lty=1,xlim=c(xmin,xmax),ylim=c(ymin,ymax),xlab="x",ylab="y")

par(new=F)

}

# Trace des courbes de reference sans puis avec lissage a posteriori

#===================================================================

graphCourbesRef(donnees,quant5, quant95)

graphCourbesRef(donnees,quant5lis,quant95lis)

# Trace du critere de validation croisee

#=======================================

plot(CV[,1],CV[,2],xlab="h",ylab="CV(h)",type="l")

La figure 1.1 représente le nuage des points et les courbes de référence à 90% sans qu’il n’y ait eu de lissage a posteriori des quantiles conditionnels. La figure 1.2 donne le graphique du critère de validation croisée ayant permis de déterminer la fenêtre optimale. Ces graphiques ont été obtenues avec le programme Splus ci-dessus.

1. Nuage de points et courbes de référence

2. Critère de validation croisée

Figure 1 : Exemple de sorties graphiques obtenues avec Splus

4.2. Interface avec SAS

/* Recuperation des donnees et des resultats dans des tables SAS */

/*****************************************************************/

data donnees;

infile 'c:\Temp\donnees.dat';

input X Y;

run;

data quantile5;

infile 'c:\Temp\est1.donnees.Qn5';

input Z qn5;

run;

data quantile95;

infile 'c:\Temp\est1.donnees.Qn95';

input Z qn95;

run;

data quantile5lis;

infile 'c:\Temp\est1.donnees.Qn5.lis';

input Z qn5lis;

run;

data quantile95lis;

infile 'c:\Temp\est1.donnees.Qn95.lis';

input Z qn95lis;

run;

data globale;

set donnees quantile5 quantile95 quantile5lis quantile95lis;

run;

data CV;

infile 'c:\windows\bureau\Modulad_C\est1.donnees.CV';

input h CV;

run;

/* Graphiques du nuage de points et des courbes de reference */

/*************************************************************/

symbol1 v=plus i=none;

symbol2 v=none i=join;

/* sans lissage a posteriori */

proc gplot data=globale;

plot Y*X=1 qn5*Z=2 qn95*Z=2 / overlay;

run; quit;

/* avec lissage a posteriori */

proc gplot data=globale;

plot Y*X=1 qn5lis*Z=2 qn95lis*Z=2 / overlay;

run; quit;

/* Graphique du critere de validation croisee */

/**********************************************/

proc gplot data=CV;

plot CV*h=2;

run; quit;

La figure 2 représente le nuage des points et les courbes de référence à 90% lorsqu’il y a eu un lissage a posteriori des quantiles conditionnels. Ces graphiques ont été obtenues avec le programme SAS ci-dessus.

Figure 2 : Exemple de sortie graphique obtenue avec SAS

4.3. Interface avec Gnuplot

Pour obtenir un graphique du type de celui présenté en figure 2 avec Gnuplot, la commande est la suivante :

plot 'donnees.dat', 'est1.donnees.Qn5.lis' with lines, 'est1.donnes.Qn95.lis' with lines

5. Application à des données réelles

L’objectif d’un projet développé par le CE.R.I.E.S. (Centre de recherche sur la peau humaine financé par Chanel) est d'établir des courbes de référence à 90% en fonction de l'âge pour des propriétés biophysiques de la peau de femmes japonaises saines sur deux zones du visage (front et joue) et une zone de l'avant-bras. Pour cela, une étude réalisée par le CE.R.I.E.S. a été conduite entre le 15 décembre 1998 et le 15 avril 1999 à Sendai (Japon) sur n=120 femmes japonaises âgées de 20 à 80 ans présentant une peau apparemment saine (c'est-à-dire sans aucun signe de dermatose en cours ou de maladie générale avec manifestations cutanées avérées). Chaque volontaire a été examinée en atmosphère (température et humidité relative) contrôlée. Cette étude comportait des questionnaires sur les habitudes de vie, un interrogatoire et un examen médical cutané, ainsi qu'une évaluation des propriétés biophysiques cutanées. Les propriétés biophysiques de la peau incluaient en particulier le taux de sécrétion de sébum (taux instantané de lipides), mesuré uniquement sur les deux zones du visage. Ces deux variables SJOUE et SFRONT sont ici les variables. La covariable est l'âge des volontaires (qui ne prend que des valeurs entières allant de 20 à 80 ans).

Les figures 3 et 4 montrent les courbes de référence à 90% qui ont été construites par les trois méthodes non paramétriques pour les variables SJOUE et SFRONT.

Figure 3 : Courbes de référence à 5% et 95% obtenues avec les méthodes non paramétriques pour la variable SFRONT (trait continu : méthode d'estimation par noyau, pointillés : méthode de la constante locale, tirets : méthode d'estimation par noyau produit).

Figure 4 : Courbes de référence à 5% et 95% obtenues avec les méthodes non paramétriques pour la variable SJOUE (trait continu : méthode d'estimation par noyau, pointillés : méthode de la constante locale, tirets : méthode d'estimation par noyau produit).

En ce qui concerne la variable SJOUE, les courbes de référence supérieures obtenues avec les trois estimateurs non paramétriques correspondent bien à ce que l'on s'attend à observer d'un point de vue biologique (décroissance du taux instantané de sébum avec l'âge), seul l'aspect légèrement « ondulé' » n'est pas totalement conforme. Pour « lisser » un peu plus ces courbes, il serait possible de prendre une fenêtre légèrement plus large que celle sélectionnée par la méthode de validation croisée.

Pour ce qui est de la variable SFRONT, les courbes de référence supérieures se comportent de manière semblable jusqu'à l'âge de 65 ans. Ensuite, le premier estimateur décroît plus rapidement que les deux autres ce qui correspond bien à une diminution attendue du taux instantané de sébum avec l'âge. En ce sens, cette courbe de référence pourrait être préférée aux deux autres.

Remerciements

Les auteurs remercient le Pr. E. Tschachler pour ses encouragements,le Pr. H. Tagami, le Dr K. Numagami et toute l'équipe du CE.R.I.E.S. pour leur contribution aux données, en particulier J. Latreille, I. Le Fur et le Dr F. Morizot.

Références bibliographiques

Gannoun, A., Girard, S., Guinot, C. & Saracco, J. (2002). ). Trois méthodes non paramétriques pour l'estimation de courbes de référence. Application à l'analyse des propriétés biophysiques de la peau. Revue de Statistique appliquée, 1, 65-89.

Yao, Q. (1999). Conditional predictive regions for stochastic processes. Technical report, University of Kent at Canterbury, UK.

Yu, K. & Jones, M.C. (1998). Local linear quantile regression. Journal of the American Statistical Association}, 93, 228-237.