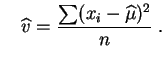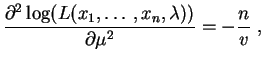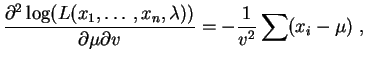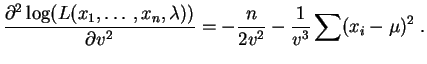Section : Recherche d'estimateurs
Précédent : Notion de vraisemblance
Suivant : Intervalles de confiance
Dans la plupart des cas d'intérêt pratique, la loi 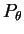 , et
donc aussi la
vraisemblance,
ont une expression dérivable par
rapport à
, et
donc aussi la
vraisemblance,
ont une expression dérivable par
rapport à 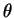 . Pour calculer le maximum de la
vraisemblance,
il faut déterminer les valeurs pour lesquelles la dérivée
de la
vraisemblance
s'annule. Or par définition, la
vraisemblance
est un produit de
probabilités
ou de
densités,
qui peut être
assez compliqué à dériver. Il est préférable
de dériver une somme, et c'est pourquoi on commence par remplacer
la
vraisemblance
par son logarithme. La fonction logarithme étant croissante,
il est équivalent de maximiser
. Pour calculer le maximum de la
vraisemblance,
il faut déterminer les valeurs pour lesquelles la dérivée
de la
vraisemblance
s'annule. Or par définition, la
vraisemblance
est un produit de
probabilités
ou de
densités,
qui peut être
assez compliqué à dériver. Il est préférable
de dériver une somme, et c'est pourquoi on commence par remplacer
la
vraisemblance
par son logarithme. La fonction logarithme étant croissante,
il est équivalent de maximiser
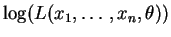 ou
ou
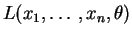 . Une fois déterminée une valeur de
. Une fois déterminée une valeur de 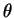 pour laquelle la dérivée s'annule, il faut s'assurer à l'aide
de la dérivée seconde que ce point est bien un maximum.
Nous traitons ci-dessous quelques familles classiques.
pour laquelle la dérivée s'annule, il faut s'assurer à l'aide
de la dérivée seconde que ce point est bien un maximum.
Nous traitons ci-dessous quelques familles classiques.
Lois de Bernoulli
L'ensemble des valeurs possibles est 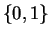 . Le paramètre
inconnu est
. Le paramètre
inconnu est 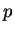 .
.
Si
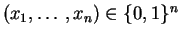 est un
échantillon, la
vraisemblance
vaut :
est un
échantillon, la
vraisemblance
vaut :
Son logarithme est :
La dérivée par rapport à 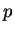 est :
Elle s'annule pour :
La dérivée seconde est :
Elle est strictement négative, la valeur
est :
Elle s'annule pour :
La dérivée seconde est :
Elle est strictement négative, la valeur
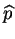 est bien un maximum.
Si
est bien un maximum.
Si
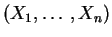 est un
échantillon
de la
loi de Bernoulli
de
paramètre
est un
échantillon
de la
loi de Bernoulli
de
paramètre 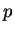 ,
l'estimateur
du
maximum de vraisemblance
de
,
l'estimateur
du
maximum de vraisemblance
de 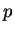 est :
à savoir la
fréquence empirique.
est :
à savoir la
fréquence empirique.
Lois géométriques
L'ensemble des valeurs possibles est
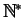 . Le paramètre
inconnu est
. Le paramètre
inconnu est ![$ p\in]0,1[$](img301.gif) .
.
Si
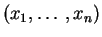 est un
échantillon
d'entiers, la
vraisemblance
vaut :
est un
échantillon
d'entiers, la
vraisemblance
vaut :
Son logarithme est :
La dérivée par rapport à 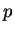 est :
Elle s'annule pour :
La dérivée seconde est :
Elle est strictement négative, la valeur
est :
Elle s'annule pour :
La dérivée seconde est :
Elle est strictement négative, la valeur
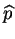 est bien un maximum.
Si
est bien un maximum.
Si
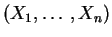 est un
échantillon
de la
loi géométrique
de
paramètre
est un
échantillon
de la
loi géométrique
de
paramètre 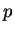 ,
l'estimateur
du
maximum de vraisemblance
de
,
l'estimateur
du
maximum de vraisemblance
de 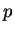 est :
à savoir l'inverse de la
moyenne empirique,
ce qui est cohérent
avec le fait que le paramètre
est :
à savoir l'inverse de la
moyenne empirique,
ce qui est cohérent
avec le fait que le paramètre 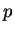 est l'inverse de
l'espérance.
est l'inverse de
l'espérance.
Lois exponentielles
Le paramètre inconnu est encore 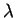 . Il s'agit ici de
lois continues,
la
vraisemblance
est donc un produit de valeurs de la
densité. Pour
un
. Il s'agit ici de
lois continues,
la
vraisemblance
est donc un produit de valeurs de la
densité. Pour
un 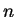 -uplet de réels positifs
-uplet de réels positifs
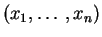 elle vaut :
elle vaut :
Son logarithme est :
La dérivée par rapport à 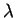 est :
Elle s'annule pour :
La dérivée seconde est :
Elle est strictement négative, la valeur
est :
Elle s'annule pour :
La dérivée seconde est :
Elle est strictement négative, la valeur
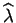 est bien
un maximum.
Si
est bien
un maximum.
Si
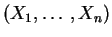 est un
échantillon
de la
loi exponentielle
de
paramètre
est un
échantillon
de la
loi exponentielle
de
paramètre 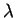 ,
l'estimateur
du
maximum de vraisemblance
de
,
l'estimateur
du
maximum de vraisemblance
de 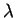 est :
à savoir l'inverse de la
moyenne empirique,
ce qui est cohérent
avec le fait que le paramètre
est :
à savoir l'inverse de la
moyenne empirique,
ce qui est cohérent
avec le fait que le paramètre 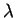 est égal à l'inverse de
l'espérance.
est égal à l'inverse de
l'espérance.
Lois normales
Pour un paramètre multidimensionnel, le principe est le même, mais
les calculs d'optimisation sont plus compliqués. Pour les lois normales,
deux paramètres sont inconnus. Afin d'éviter les confusions dans
les dérivations, nous noterons 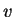 le paramètre de
variance,
habituellement noté
le paramètre de
variance,
habituellement noté 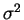 .
Pour un
.
Pour un 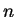 -uplet de réels
-uplet de réels
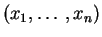 la
vraisemblance
vaut :
la
vraisemblance
vaut :
Son logarithme est :
Les dérivées partielles par rapport aux paramètres 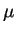 et
et 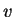 sont :
et
Elle s'annulent pour :
sont :
et
Elle s'annulent pour :
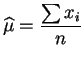
et
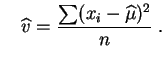
Les dérivées partielles secondes valent :
La matrice hessienne (matrice des dérivées partielles secondes)
au point
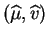 est donc :
Elle est définie négative, le point
est donc :
Elle est définie négative, le point
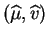 est
bien un maximum.
Si
est
bien un maximum.
Si
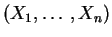 est un
échantillon
de la
loi normale
de
paramètres
est un
échantillon
de la
loi normale
de
paramètres 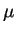 et
et 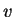 , les
estimateurs
du
maximum de vraisemblance
de
, les
estimateurs
du
maximum de vraisemblance
de
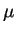 et
et 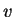 sont respectivement la
moyenne
et la
variance
empiriques de
l'échantillon,
comme on pouvait s'y attendre.
sont respectivement la
moyenne
et la
variance
empiriques de
l'échantillon,
comme on pouvait s'y attendre.
Section : Recherche d'estimateurs
Précédent : Notion de vraisemblance
Suivant : Intervalles de confiance
![]() , et
donc aussi la
vraisemblance,
ont une expression dérivable par
rapport à
, et
donc aussi la
vraisemblance,
ont une expression dérivable par
rapport à ![]() . Pour calculer le maximum de la
vraisemblance,
il faut déterminer les valeurs pour lesquelles la dérivée
de la
vraisemblance
s'annule. Or par définition, la
vraisemblance
est un produit de
probabilités
ou de
densités,
qui peut être
assez compliqué à dériver. Il est préférable
de dériver une somme, et c'est pourquoi on commence par remplacer
la
vraisemblance
par son logarithme. La fonction logarithme étant croissante,
il est équivalent de maximiser
. Pour calculer le maximum de la
vraisemblance,
il faut déterminer les valeurs pour lesquelles la dérivée
de la
vraisemblance
s'annule. Or par définition, la
vraisemblance
est un produit de
probabilités
ou de
densités,
qui peut être
assez compliqué à dériver. Il est préférable
de dériver une somme, et c'est pourquoi on commence par remplacer
la
vraisemblance
par son logarithme. La fonction logarithme étant croissante,
il est équivalent de maximiser
![]() ou
ou
![]() . Une fois déterminée une valeur de
. Une fois déterminée une valeur de ![]() pour laquelle la dérivée s'annule, il faut s'assurer à l'aide
de la dérivée seconde que ce point est bien un maximum.
Nous traitons ci-dessous quelques familles classiques.
pour laquelle la dérivée s'annule, il faut s'assurer à l'aide
de la dérivée seconde que ce point est bien un maximum.
Nous traitons ci-dessous quelques familles classiques.
![]() . Le paramètre
inconnu est
. Le paramètre
inconnu est ![]() .
.
![]() est un
échantillon, la
vraisemblance
vaut :
est un
échantillon, la
vraisemblance
vaut :
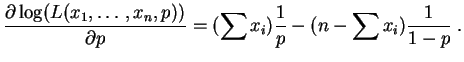
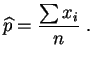
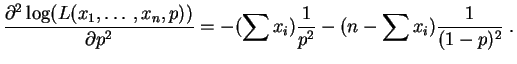
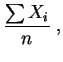
![]() . Le paramètre
inconnu est
. Le paramètre
inconnu est ![]() .
.
![]() est un
échantillon
d'entiers, la
vraisemblance
vaut :
est un
échantillon
d'entiers, la
vraisemblance
vaut :
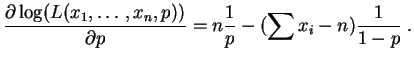
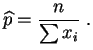
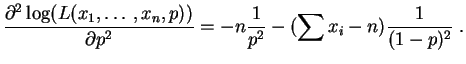
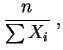
![]() . Il s'agit ici de
lois continues,
la
vraisemblance
est donc un produit de valeurs de la
densité. Pour
un
. Il s'agit ici de
lois continues,
la
vraisemblance
est donc un produit de valeurs de la
densité. Pour
un ![]() -uplet de réels positifs
-uplet de réels positifs
![]() elle vaut :
elle vaut :
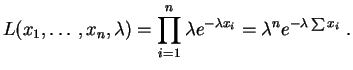
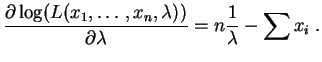
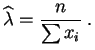
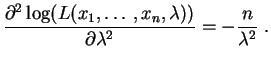
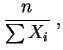
![]() le paramètre de
variance,
habituellement noté
le paramètre de
variance,
habituellement noté ![]() .
Pour un
.
Pour un ![]() -uplet de réels
-uplet de réels
![]() la
vraisemblance
vaut :
la
vraisemblance
vaut :
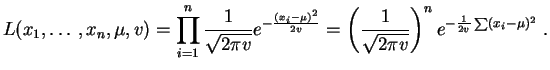
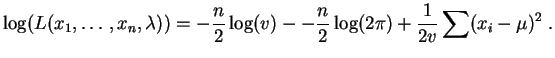
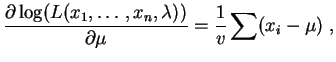
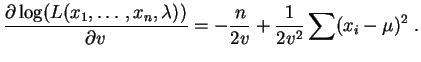
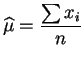 et
et