Section : Variables aléatoires
Précédent : Variables aléatoires continues
Suivant : Fonction quantile
Fonction de répartition
La
fonction de répartition
d'une
variable aléatoire
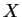 à valeurs dans
à valeurs dans
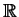 (ou plus exactement de sa loi) est la fonction
(ou plus exactement de sa loi) est la fonction 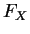 , de
, de
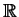 dans
dans
![$ [0,1]$](img50.gif) , qui à
, qui à
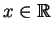 associe :
associe :
Les propriétés principales sont les suivantes.
Lois discrètes.
La
fonction de répartition
d'une
variable aléatoire discrète
est une
fonction en escalier. Si la
variable aléatoire
prend les valeurs
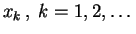 , supposées rangées par ordre croissant, alors la
fonction de répartition
, supposées rangées par ordre croissant, alors la
fonction de répartition
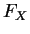 prend les valeurs :
prend les valeurs :
Voici par exemple la loi et les valeurs différentes de la fonction de
répartition pour le nombre de bons numéros pour 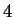 numéros cochés
sur une grille de Kéno.
numéros cochés
sur une grille de Kéno.
Si 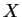 suit la
loi géométrique
suit la
loi géométrique
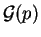 , sa fonction de répartition
, sa fonction de répartition
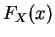 vaut 0 pour
vaut 0 pour 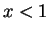 . Pour tout
. Pour tout 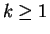 , elle est constante sur
l'intervalle
, elle est constante sur
l'intervalle 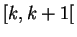 et vaut :
A part les lois
géométriques,
les fonctions de répartitions des lois
discrètes classiques n'ont pas d'expression analytique simple.
et vaut :
A part les lois
géométriques,
les fonctions de répartitions des lois
discrètes classiques n'ont pas d'expression analytique simple.
Lois continues.
La
fonction de répartition
d'une
variable aléatoire continue
est la
primitive de la
densité
qui s'annule en 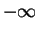 :
:
C'est une fonction continue sur
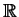 . En tout point
. En tout point 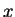 où
où 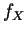 est
continue,
est
continue, 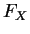 est dérivable et :
Reprenons les trois exemples de base.
est dérivable et :
Reprenons les trois exemples de base.
Loi
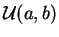
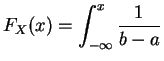 1
1![$\displaystyle _{[a,b]}(t)dt
= \left\{
\begin{array}{cl}
0 & \mbox{si } x\leq a ...
...
& \mbox{si } x\in [a,b]
\\
1 & \mbox{si } x\geq b
\;.
\end{array}\right.
$](img398.gif)
Loi
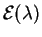
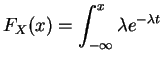 1
1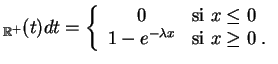
Loi
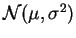
Il n'existe pas d'expression analytique pour la
fonction de répartition
des
lois normales. On en trouve des valeurs approchées dans les tables. La
plupart des langages spécialisés ont un code d'intégration numérique
qui calcule 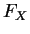 , pour les lois normales comme pour toutes les lois
usuelles.
, pour les lois normales comme pour toutes les lois
usuelles.
La
fonction de répartition
est l'outil privilégié des calculs de lois.
Un cas fréquent dans les applications est celui où on connaît la loi
de 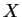 et on veut déterminer la loi de
et on veut déterminer la loi de
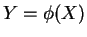 . Voici quelques
exemples standard.
. Voici quelques
exemples standard.
- Dans le cas où
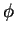 est dérivable, strictement croissante.
La
densité
correspondante est :
est dérivable, strictement croissante.
La
densité
correspondante est :
- Si
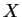 suit la loi
suit la loi
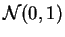 et
et
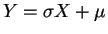 , avec
, avec
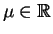 ,
,
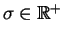 .
La
densité
correspondante est :
et donc Y suit la loi
.
La
densité
correspondante est :
et donc Y suit la loi
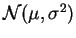 . Ceci permet de ramener les
calculs de
probabilité
sur une
loi normale
quelconque aux calculs sur la loi
. Ceci permet de ramener les
calculs de
probabilité
sur une
loi normale
quelconque aux calculs sur la loi
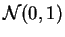 .
.
- Si
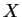 suit la loi
suit la loi
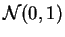 et
et 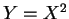 .
.
![$\displaystyle F_Y(y)
=P[X^2<Y]
=0 \,\,$](img410.gif)
si
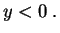
Si 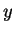 est positif :
est positif :
![$\displaystyle F_Y(y)
=P[-\sqrt y\leq X\leq +\sqrt y]
=F_X(\sqrt y)-F_X(-\sqrt y)\,\,$](img412.gif)
si
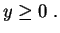
La
densité
correspondante est :
La loi de
densité
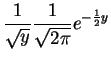 1
1
est la
loi de chi-deux
à 1 degré de liberté
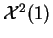 . C'est
aussi la
loi gamma
. C'est
aussi la
loi gamma
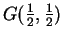 .
.
Section : Variables aléatoires
Précédent : Variables aléatoires continues
Suivant : Fonction quantile
![]() à valeurs dans
à valeurs dans
![]() (ou plus exactement de sa loi) est la fonction
(ou plus exactement de sa loi) est la fonction ![]() , de
, de
![]() dans
dans
![]() , qui à
, qui à
![]() associe :
associe :
![]() , supposées rangées par ordre croissant, alors la
fonction de répartition
, supposées rangées par ordre croissant, alors la
fonction de répartition
![]() prend les valeurs :
prend les valeurs :
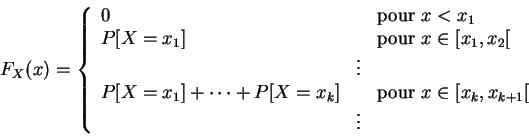
![]() numéros cochés
sur une grille de Kéno.
numéros cochés
sur une grille de Kéno.
![]() :
:
![$\displaystyle F_X(x) = P[X\leq x] = \int_{-\infty}^x f_X(t)\,dt\;.
$](img395.gif)
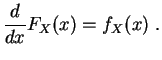
![]()
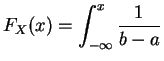 1
1![$\displaystyle _{[a,b]}(t)dt
= \left\{
\begin{array}{cl}
0 & \mbox{si } x\leq a ...
...
& \mbox{si } x\in [a,b]
\\
1 & \mbox{si } x\geq b
\;.
\end{array}\right.
$](img398.gif)
![]()
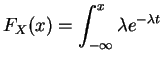 1
1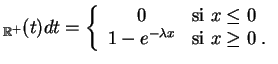
![]()
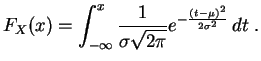
![]() et on veut déterminer la loi de
et on veut déterminer la loi de
![]() . Voici quelques
exemples standard.
. Voici quelques
exemples standard.
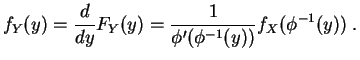
![$\displaystyle F_Y(y)
=P[\sigma X+\mu\leq y]
=P\left[X\leq \frac{y-\mu}{\sigma}\right]
=F_X\left(\frac{y-\mu}{\sigma }\right)\;.
$](img407.gif)
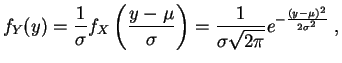
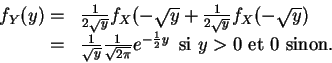
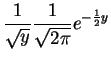 1
1