Section : Données unidimensionnelles
Précédent : Moyenne empirique
Suivant : Distribution empirique

Variance empirique

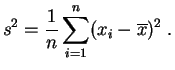
Les notions de variance et d'écart-type servent à quantifier la dispersion d'un échantillon autour de sa moyenne. La définition est la suivante :

Définition 1.4   Soit $(x_1,\ldots,x_n)$ un échantillon, et $\overline{x}$ sa moyenne empirique. On appelle variance de l'échantillon, la quantité, notée $s^2$, définie par :

$$s^2 = \frac{1}{n} \sum_{i=1}^n (x_i-\overline{x})^2\;.$$

On appelle écart-type de l'échantillon la racine carrée de la variance.

L'avantage de l'écart-type sur la variance est qu'il s'exprime, comme la moyenne, dans la même unité que les données. On utilise parfois le coefficient de variation, qui est le rapport de l'écart-type sur la moyenne.

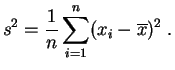
Pour mesurer la dispersion d'un échantillon autour de sa moyenne, on pourrait trouver plus naturelle une autre mesure d'écart, par exemple l'écart absolu moyen dont nous parlerons plus loin. La raison pour laquelle la définition ci-dessus est la plus naturelle tient dans la proposition suivante.

Proposition 1.5   Soit $(x_1,\ldots,x_n)$ un échantillon numérique. Considérons l'application $EQ$ (erreur quadratique) qui à un nombre $m$ associe :

$$EQ(m) = \frac{1}{n} \sum_{i=1}^n (x_i-m)^2\;.$$

L'application $EQ$ admet un minimum absolu pour $m=\overline{x}$. La valeur de ce minimum est la variance de l'échantillon.

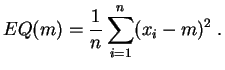
Le choix de la variance pour mesurer la dispersion d'un échantillon est donc cohérent avec celui de la moyenne empirique comme valeur centrale. Nous verrons plus loin qu'un phénomène analogue a lieu pour l'écart absolu moyen et la médiane.

Démonstration : La fonction $EQ(m)$ est un polynôme de degré deux en $m$ :

$$EQ(m) = m^2 - 2m \overline{x} +\frac{1}{n} \sum_{i=0}^n x_i^2\;.$$

Elle est décroissante, puis croissante, et atteint son minimum au point où la dérivée s'annule, à savoir $m=\overline{x}$.$\square$

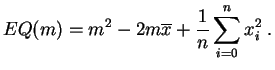
Pour le calcul algorithmique, on calcule en général simultanément moyenne et variance grâce à la formule suivante.

Proposition 1.6   On a :

$$s^2 = \Big(\frac{1}{n} \sum_{i=0}^n x_i^2\Big) - \overline{x}^2\;.$$

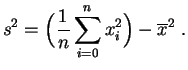
Démonstration :Il suffit de développer les carrés dans la définition de $s^2$ :

$$\begin{array}{ccc} s^2&=&\frac{1}{n} \sum_{i=1}^n (x_i-\overl... ...ac{1}{n} \sum_{i=0}^n x_i^2\Big) -\overline{x}^2\;. \end{array}$$

$\square$

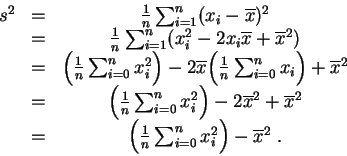
Dans le cas particulier des données binaires, codées sur 0 et 1, la moyenne est la fréquence de 1, et la variance n'apporte aucune information supplémentaire. En effet, si tous les $x_i$ valent 0 ou 1, alors $x_i^2=x_i$ et donc :

$$s^2 = \overline{x} - \overline{x}^2 = \overline{x}(1-\overline{x})\;.$$

Dans le cas général, l'algorithme de calcul est le suivant.

somme1 $\longleftarrow 0$
somme2 $\longleftarrow 0$
Pour $i$ de 1 à $n$
somme1 $\longleftarrow$ somme1$+ x_i$
somme2 $\longleftarrow$ somme2$+ x_i^2$
finPour
moyenne $\longleftarrow$ somme1$/n$
variance $\longleftarrow$ somme2$/n -$ moyenne $*$moyenne

Pour les très gros échantillons, il faut prendre garde à l'imprécision des sommes cumulées. Pour éviter des erreurs, on aura intérêt à travailler en double précision ou même à remplacer la boucle par deux boucles emboîtées. Dans certains cas, on pourra simplifier les calculs en utilisant l'invariance par translation. Si pour tout $i=1,\ldots,n$ on pose $y_i=ax_i+b$, alors la variance de $(y_1,\ldots,y_n)$ est $a^2s^2$. Soit par exemple l'échantillon suivant :

$$(98765420\,,\; 98765430\,,\; 98765410\,,\; 98765400)\;.$$

Il est plus facile, et plus stable numériquement, de calculer la moyenne et la variance de l'échantillon $(2, 3, 1, 0)$.

Une fois la moyenne calculée, nous avons vu qu'on pouvait centrer les données pour se ramener à une moyenne nulle. La variance des données centrées est la même que celle de l'échantillon initial. Une fois cette variance calculée, on peut réduire les données centrées en les divisant par l'écart-type. On obtient ainsi un nouvel échantillon dont la moyenne est nulle et la variance égale à 1. On parle d'échantillon réduit. Remarquons que les données réduites sont des nombres sans unité. On peut donc comparer deux échantillons réduits, même si les données initiales n'étaient pas exprimées dans la même unité.

L'inconvénient de l'écart-type tel qu'il a été défini jusque là, est qu'il a tendance à sous-estimer légèrement l'écart des données par rapport à leur moyenne. La raison mathématique de ce défaut est liée à la notion de biais d'un estimateur. On peut en saisir la raison intuitive sur un exemple simple. Supposons que l'on joue trois fois à un jeu dont l'enjeu est 1 franc. Chaque résultat vaut donc $\pm 1$. Si le jeu est équitable, on s'attend à ce que la moyenne vaille 0 et l' écart-type 1. Or sur trois parties, les résultats possibles à l'ordre près sont les suivants.

$(x_1,x_2,x_3)$	$\overline{x}$	$s^2$
(-1,-1,-1)	-1	0
(-1,-1,1)	-1/3	8/9
(-1,1,1)	1/3	8/9
(1,1,1)	1	0

En aucun cas l' écart-type empirique ne peut atteindre 1. Le moyen de corriger cette sous-estimation systématique est de multiplier la variance par $n/(n\!-\!1)$, où $n$ est la taille de l'échantillon. On parle alors de variance non biaisée. C'est la raison de la présence sur certaines calculatrices de deux touches de calcul de l'écart-type, une marquée $\sigma_n$ (notre $s$), l'autre $\sigma_{n-1}$, qui retourne $s\sqrt{\frac{n}{n-1}}$.

Section : Données unidimensionnelles
Précédent : Moyenne empirique
Suivant : Distribution empirique