Section : Intervalles de confiance
Précédent : Modèle linéaire

Normalité asymptotique

La construction des intervalles de confiance nécessite de connaître la loi des estimateurs à partir desquels ils sont construits. En dehors du cas des échantillons gaussiens, ce n'est pas toujours possible. De plus, il est fréquent que les calculs de lois, effectivement implémentables pour de petits échantillons, deviennent infaisables pour un échantillon de grande taille. On cherche alors à remplacer la loi de l'estimateur par une approximation plus simple, permettant de construire des intervalles de confiance dont le niveau n'est garanti que asymptotiquement.

Définition 3.5   Soit $ (X_1,\ldots,X_n)$ un échantillon de la loi $ P_\theta$. Pour tout $ n$, soient $ T_{1,n}\leq T_{2,n}$ deux statistiques, fonction de l'échantillon $ (X_1,\ldots,X_n)$.
On dit que $ [T_{1,n}\,,\,T_{2,n}]$ est un intervalle de confiance, de niveau asymptotique $ 1\!-\!\alpha$ pour $ \theta$, si :

$\displaystyle \lim_{n\rightarrow\infty}\mathbb{P}[ \theta \in [T_{1,n}\,,\,T_{2,n}]\,]=1-\alpha\;. $

Le plus souvent, cette notion est utilisée quand on dispose d'un estimateur convergent de $ \theta$ dont la loi est asymptotiquement normale, ce qui est en général une conséquence du théorème central limite.

Nous traitons tout d'abord le cas de l'estimation de l'espérance.

Théorème 3.6   Soit $ (X_1,\ldots,X_n)$ un échantillon d'une loi de probabilité d'espérance $ \mu$, de variance $ \sigma^2$. Soit $ \overline{X}_n$ sa moyenne empirique et $ S^2_n$ sa variance empirique. Posons :

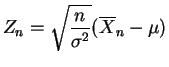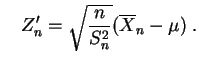
$\displaystyle Z_n = \sqrt{\frac{n}{\sigma^2}}(\overline{X}_n-\mu)$   et$\displaystyle \quad Z'_n = \sqrt{\frac{n}{S^2_n}}(\overline{X}_n-\mu)\;. $

Les lois des variables aléatoires $ Z_n$ et $ Z'_n$ convergent vers la loi normale $ {\cal N}(0,1)$.

Ce résultat, qui est une reformulation du théorème central limite classique, permet de définir des intervalles de dispersion approchés pour $ Z_n$ et $ Z'_n$. Fixons le niveau $ 1\!-\!\alpha$, et notons $ [-z_\alpha\,,\,z_\alpha]$ l'intervalle de dispersion optimal de la loi $ {\cal N}(0,1)$. Alors :

$\displaystyle \lim_{n\rightarrow\infty} \mathbb{P}[\, Z_n\in [-z_\alpha\,,\,z_\... ...htarrow\infty} \mathbb{P}[\, Z'_n\in [-z_\alpha\,,\,z_\alpha]\, ] =1-\alpha\;. $

On en déduit immédiatement deux intervalles de confiance, de niveau asymptotique $ 1\!-\!\alpha$ pour $ \mu$ :

$\displaystyle \left[\,\overline{X}_n-z_\alpha\sqrt{\frac{\sigma^2}{n}}\,,\, \overline{X}_n+z_\alpha\sqrt{\frac{\sigma^2}{n}}\,\right]$   et$\displaystyle \quad \left[\,\overline{X}_n-z_\alpha\sqrt{\frac{S^2_n}{n}}\,,\, \overline{X}_n+z_\alpha\sqrt{\frac{S^2_n}{n}}\,\right]\;. $


Les utilisations de la normalité asymptotique vont bien au-delà de l'estimation des moyennes. A titre d'exemple, nous traitons ci-dessous l'estimation des quantiles d'une loi continue. Considérons un échantillon $ (X_1,\ldots,X_n)$ d'une loi continue. Nous noterons $ f$ sa densité, $ F$ sa fonction de répartition et $ Q$ sa fonction quantile. Etant donnée une valeur $ u\in]0,1[$, le problème consiste à estimer $ Q(u)$ (par exemple, si $ u=0.5$, $ Q(u)$ est la médiane). A l'échantillon $ (X_1,\ldots,X_n)$ est associée une fonction quantile empirique. Sa valeur en $ u$ est la $ i$-ième statistique d'ordre $ X_{(i)}$, où $ i$ est l'entier tel que $ i\!-\!1<nu\leq i$. Nous noterons $ T_n$ cette variable aléatoire. C'est un estimateur convergent de $ Q(u)$. On peut écrire explicitement sa densité en fonction de $ f$ et $ F$ :

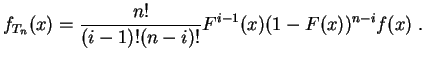
$\displaystyle f_{T_n}(x) = \frac{n!}{(i-1)!(n-i)!}F^{i-1}(x)(1-F(x))^{n-i}f(x)\;. $

Cependant, il n'y a pas en général d'expression explicite pour la fonction de répartition ni pour la fonction quantile de $ T_n$, et le calcul numérique des intervalles de dispersion peut être assez problématique pour de grandes valeurs de $ n$. On démontre que la loi de $ T_n$ est asymptotiquement normale.

Théorème 3.7   Posons :

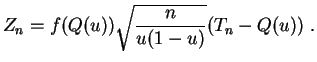
$\displaystyle Z_n = f(Q(u))\sqrt{\frac{n}{u(1-u)}}(T_n-Q(u))\;. $

La loi de $ Z_n$ converge vers la loi normale $ {\cal N}(0,1)$.

Un intervalle de confiance de niveau asymptotique $ 1\!-\!\alpha$ pour $ Q(u)$ sera donc :

$\displaystyle \left[\,T_n - z_\alpha \frac{\sqrt{u(1-u)}}{f(Q(u))\sqrt{n}}\,,\, T_n + z_\alpha \frac{\sqrt{u(1-u)}}{f(Q(u))\sqrt{n}}\,\right]\;. $

En pratique, la taille de l'échantillon, même grande, est toujours fixée. Dans l'utilisation de la normalité asymptotique, la question se pose évidemment de la qualité de l'approximation normale à $ n$ fixé. A partir de quelle valeur de $ n$ est-il légitime de remplacer une loi exacte par son approximation normale pour un calcul d'intervalle de confiance ? Il est impossible de donner des bornes valables dans toutes les situations. A titre d'exemple, nous considèrerons trois familles de lois asymptotiquement normales, les lois binomiales, les lois de Poisson et les lois lois gamma (incluant les lois du chi-deux comme cas particulier). La loi $ {\cal B}(n,p)$, la loi $ {\cal P}(n)$ et la loi $ {\cal G}(n,\lambda)$ sont proches de la loi normale de même espérance et de même variance, quand $ n$ est grand. Le tableau ci-dessous donne les distances de Kolmogorov-Smirnov entre quelques unes de ces lois et leurs approximations normales (la distance de Kolmogorov-Smirnov est la différence maximale en valeur absolue entre fonctions de répartition).

Loi
$ {\cal B}(10,0.5)$
$ {\cal B}(10,0.2)$
$ {\cal B}(100,0.2)$
$ {\cal P}(30)$
$ {\cal P}(100)$
$ {\cal P}(200)$
$ D_{KS}$
0.0027
0.0295
0.0099
0.0121
0.0066
0.0047
Loi
$ {\cal G}(10,1)$
$ {\cal G}(50,1)$
$ {\cal G}(100,1)$
$ {\cal X}^2(30)$
$ {\cal X}^2(50)$
$ {\cal X}^2(100)$
$ D_{KS}$
0.0420
0.0188
0.0133
0.0344
0.0266
0.0188

Les environnements de calcul sont désormais capables d'effectuer des calculs précis de n'importe quel quantile pour toutes les lois usuelles. En règle générale, il faut éviter d'utiliser la normalité asymptotique quand un calcul exact est possible.


Section : Intervalles de confiance
Précédent : Modèle linéaire