Les
échantillons
gaussiens
sont souvent utilisés pour modéliser
les erreurs dans les
modèles de
régression.
Ces modèles visent
à expliquer un
caractère
![]() (considéré comme aléatoire)
par des caractères
(déterministes)
(considéré comme aléatoire)
par des caractères
(déterministes)
![]() . On choisit une fonction
de régression
. On choisit une fonction
de régression ![]() , dépendant en général de plusieurs paramètres
inconnus, et on écrit les
variables aléatoires
, dépendant en général de plusieurs paramètres
inconnus, et on écrit les
variables aléatoires
![]() sous la forme :
sous la forme :
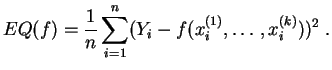
Nous considérons seulement la régression linéaire simple :
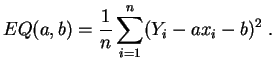
On obtient ainsi les estimateurs des moindres carrés :
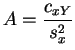 et
etL'erreur quadratique minimale est :
Ces trois
variables aléatoires
sont des
estimateurs convergents
de ![]() ,
, ![]() et
et ![]() respectivement. Les deux premiers sont non
biaisés.
L'espérance
de
respectivement. Les deux premiers sont non
biaisés.
L'espérance
de ![]() est
est
![]() , il est donc
asymptotiquement sans
biais.
On obtient un
estimateur sans biais
et
convergent de
, il est donc
asymptotiquement sans
biais.
On obtient un
estimateur sans biais
et
convergent de ![]() en posant :
en posant :
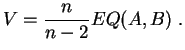
La prédiction est le premier objectif d'un
modèle
probabiliste. Dans le cas de la
régression linéaire,
si
un nouvel
individu
était examiné, avec une valeur observée ![]() pour le
caractère
pour le
caractère
![]() , le
modèle
entraîne que la valeur
, le
modèle
entraîne que la valeur ![]() du
caractère
expliqué sur cet
individu
est une
variable aléatoire,
de
loi normale
du
caractère
expliqué sur cet
individu
est une
variable aléatoire,
de
loi normale
![]() . Les paramètres de cette
loi auront pour
estimateurs
. Les paramètres de cette
loi auront pour
estimateurs
![]() et
et ![]() respectivement.
respectivement.
Le théorème suivant permet de calculer les lois de ces estimateurs, et donc des intervalles de confiance. On peut le considérer comme une extension du théorème 3.3.
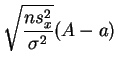 suit la
loi normale
suit la
loi normale
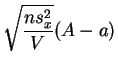 suit la
loi de Student
suit la
loi de Student
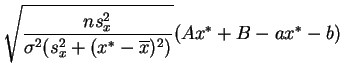 suit la
loi normale
suit la
loi normale
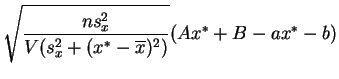 suit la
loi de Student
suit la
loi de Student
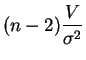 suit la
loi du chi-deux
suit la
loi du chi-deux
![$\displaystyle \left[\,A-z_\alpha\sqrt{\frac{\sigma^2}{ns_x^2}}\;,\;
A+z_\alpha\sqrt{\frac{\sigma^2}{ns_x^2}}\,\right]\;.
$](img408.gif)
![$\displaystyle \left[\,A-t_\alpha\sqrt{\frac{V}{ns_x^2}}\;,\;
A+t_\alpha\sqrt{\frac{V}{ns_x^2}}\,\right]\;.
$](img409.gif)
![$\displaystyle \left[\,Ax_*+B-z_\alpha
\sqrt{\frac{\sigma^2(s_x^2+(x^*-\overline...
..._\alpha\sqrt{\frac{\sigma^2(s_x^2+(x^*-\overline{x})^2)}{ns_x^2}}
\,\right]\;.
$](img411.gif)
![$\displaystyle \left[\,Ax_*+B-t_\alpha
\sqrt{\frac{V(s_x^2+(x^*-\overline{x})^2)...
...x_*+B+t_\alpha\sqrt{\frac{V(s_x^2+(x^*-\overline{x})^2)}{ns_x^2}}
\,\right]\;.
$](img412.gif)
![$\displaystyle \left[\,(n-2)\frac{V}{v_\alpha}\;,\;(n-2)\frac{V}{u_\alpha}\,\right]\;.
$](img413.gif)
![$\displaystyle \left[\,Ax_*\!+\!B-t_\alpha
\sqrt{\frac{V((n\!+\!1)s_x^2+(x^*\!-\...
...
\sqrt{\frac{V((n\!+\!1)s_x^2+(x^*\!-\!\overline{x})^2)}{ns_x^2}}
\,\right]\,.
$](img416.gif)
Les caractéristiques numériques prennent les valeurs suivantes :
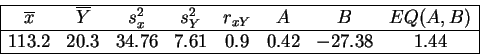
Effectuer une régression linéaire signifie que l'on pense que le poids doit croître en gros proportionnellement à la taille. La droite de régression linéaire constitue un modèle de prédiction. Pour un enfant de taille donnée, on donnera un intervalle de poids, considéré comme ``normal'', la normalité étant définie par référence au modèle et aux données. Voici les intervalles de prédiction de niveau 0.95 pour différentes tailles.
Les intervalles de prédiction sont
d'autant moins précis que la taille de
l'échantillon
initial était
faible et que la valeur de ![]() est plus éloignée de
est plus éloignée de
![]() .
.
Les résultats qui précèdent s'étendent aux régressions linéaires multiples. Les expressions explicites des intervalles de confiance sont trop compliquées pour être reproduites ici, mais elles sont programmées dans tous les logiciels de statistique standard.