Ce paragraphe est consacré à la construction
d'intervalles de confiance
de la
moyenne
et la
variance, pour les échantillons
gaussiens,
autrement dit les
échantillons
de la
loi normale
![]() . L'avantage de cette situation est
que les
estimateurs
naturels de
l'espérance
et de la
variance
ont des
lois explicitement calculables. Nous notons
. L'avantage de cette situation est
que les
estimateurs
naturels de
l'espérance
et de la
variance
ont des
lois explicitement calculables. Nous notons
![]() un
échantillon
de la loi
un
échantillon
de la loi
![]() ,
,
![]() sa
moyenne empirique
et
sa
moyenne empirique
et ![]() sa
variance empirique
.
sa
variance empirique
.
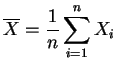 et
et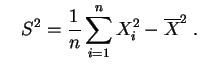
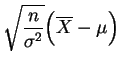 suit la
loi normale
suit la
loi normale
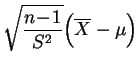 suit la
loi de Student
suit la
loi de Student
![$\displaystyle \mathbb{P}\left[\,\sqrt{\frac{n}{\sigma^2}}\Big(\overline{X}-\mu\Big)
\in[-z_\alpha,z_\alpha]\,\right] =1-\alpha\;.
$](img374.gif)
![\begin{displaymath}\begin{array}{ccc}
\sqrt{\frac{n}{\sigma^2}}\Big(\overline{X}...
...e{X}+z_\alpha\sqrt{\frac{\sigma^2}{n}}\,\right]\;.
\end{array}\end{displaymath}](img375.gif)
L'intervalle :
![$\displaystyle \left[\,\overline{X}-z_\alpha\sqrt{\frac{\sigma^2}{n}}\,,\,
\overline{X}+z_\alpha\sqrt{\frac{\sigma^2}{n}}\,\right]\;,
$](img376.gif)
Le cas où ![]() est inconnu se traite de la même façon, en
remplaçant la loi
est inconnu se traite de la même façon, en
remplaçant la loi
![]() par la loi
par la loi
![]() . C'est
encore une loi symétrique, pour laquelle
l'intervalle de dispersion
optimal de niveau
. C'est
encore une loi symétrique, pour laquelle
l'intervalle de dispersion
optimal de niveau
![]() est de la forme
est de la forme
![]() ,
où :
,
où :
![$\displaystyle \left[\,\overline{X}-t_\alpha\sqrt{\frac{S^2}{n-1}}\,,\,
\overline{X}+t_\alpha\sqrt{\frac{S^2}{n-1}}\,\right]\;.
$](img380.gif)
Passons maintenant à
l'estimation
de ![]() à partir de
à partir de ![]() .
La
loi du chi-deux
.
La
loi du chi-deux
![]() n'est pas symétrique, et
l'intervalle de dispersion
symétrique n'est pas optimal. Nous noterons
n'est pas symétrique, et
l'intervalle de dispersion
symétrique n'est pas optimal. Nous noterons
![]() et
et ![]() deux réels positifs tels que
deux réels positifs tels que
![]() soit un
intervalle de dispersion
de niveau
soit un
intervalle de dispersion
de niveau
![]() pour la loi
pour la loi
![]() . On pourra calculer
l'intervalle de dispersion
optimal
par une procédure d'optimisation numérique, ou bien prendre
l'intervalle symétrique :
. On pourra calculer
l'intervalle de dispersion
optimal
par une procédure d'optimisation numérique, ou bien prendre
l'intervalle symétrique :
![$\displaystyle \mathbb{P}\left[\,\frac{nS^2}{\sigma^2} \in [u_\alpha\,,\,v_\alpha] \,\right]
= 1-\alpha\;.
$](img386.gif)
![$\displaystyle \frac{nS^2}{\sigma^2} \in [u_\alpha,v_\alpha]\;\Longleftrightarro...
...sigma^2\in \left[\,\frac{nS^2}{v_\alpha}\,,\,\frac{nS^2}{u_\alpha}\,\right]\;.
$](img387.gif)
![$ \left[\,\frac{nS^2}{v_\alpha}\,,\,\frac{nS^2}{u_\alpha}\,\right]$](img388.gif) est donc un
intervalle de confiance
de niveau
est donc un
intervalle de confiance
de niveau