Considérons encore une
loi de probabilité
![]() dépendant du
paramètre inconnu
dépendant du
paramètre inconnu ![]() , et un
échantillon
, et un
échantillon
![]() de cette loi.
de cette loi.
Soit ![]() une fonction de
une fonction de
![]() dans
dans
![]() . Si
. Si ![]() est une variable aléatoire
de loi
est une variable aléatoire
de loi ![]() , la loi de
, la loi de ![]() dépend aussi en général de
dépend aussi en général de ![]() ,
et il en est de même de son
espérance.
Mais
,
et il en est de même de son
espérance.
Mais
![]() peut être estimée par la
moyenne empirique
de
peut être estimée par la
moyenne empirique
de
![]() .
Si
.
Si ![]() s'exprime en fonction de
s'exprime en fonction de
![]() , on en déduira alors
un
estimateur
de
, on en déduira alors
un
estimateur
de ![]() . Nous avons déjà utilisé cette
technique plusieurs fois dans les deux paragraphes précédents.
Dans la plupart des cas,
. Nous avons déjà utilisé cette
technique plusieurs fois dans les deux paragraphes précédents.
Dans la plupart des cas, ![]() est une
puissance
de
est une
puissance
de ![]() , ou de
, ou de
![]() .
Les quantités
.
Les quantités
![]() et
et
![]() s'appellent les
moments de
s'appellent les
moments de ![]() , d'où le nom de la méthode. Nous donnons trois
exemples d'application, aux lois
gamma,
béta, et
binomiale négative.
, d'où le nom de la méthode. Nous donnons trois
exemples d'application, aux lois
gamma,
béta, et
binomiale négative.
Si ![]() suit la
loi gamma
de paramètres
suit la
loi gamma
de paramètres ![]() et
et ![]() , son
espérance
et sa
variance
valent :
, son
espérance
et sa
variance
valent :
![$\displaystyle \mathbb{E}[X] = \frac{a}{\lambda}$](img161.gif) et
et![$\displaystyle \quad
Var[X] = \frac{a}{\lambda^2}\;.
$](img162.gif)
![$\displaystyle a=\frac{\mathbb{E}[X]^2}{Var[X]}$](img164.gif) et
et![$\displaystyle \quad
\lambda=\frac{\mathbb{E}[X]}{Var[X]}\;.
$](img165.gif)
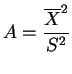 et
et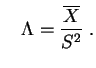
La même technique permet d'estimer les paramètres d'une
loi béta.
Si ![]() suit la
loi béta
de paramètres
suit la
loi béta
de paramètres ![]() et
et ![]() , son
espérance
et sa
variance
valent :
, son
espérance
et sa
variance
valent :
![$\displaystyle \mathbb{E}[X] = \frac{a}{a+b}$](img171.gif) et
et![$\displaystyle \quad
Var[X] = \frac{a b}{(a+b)^2(a+b+1)}\;.
$](img172.gif)
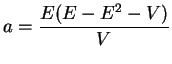 et
et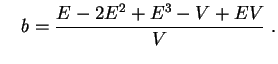
Si on dispose d'un
échantillon
de la
loi béta
de
paramètres ![]() et
et ![]() , la
moyenne empirique
, la
moyenne empirique
![]() et
la
variance empirique
et
la
variance empirique
![]() sont des
estimateurs convergents
de
sont des
estimateurs convergents
de
![]() et
et ![]() respectivement. On en déduit deux
estimateurs convergents
de
respectivement. On en déduit deux
estimateurs convergents
de ![]() et
et ![]() en remplaçant
en remplaçant ![]() et
et ![]() par
leurs
estimateurs
par
leurs
estimateurs
![]() et
et ![]() dans les expressions ci-desssus.
dans les expressions ci-desssus.
Appliquons à nouveau la technique à une
loi binomiale négative.
Si ![]() suit la
loi binomiale négative
de paramètres
suit la
loi binomiale négative
de paramètres ![]() et
et ![]() ,
son
espérance
et sa
variance
valent :
,
son
espérance
et sa
variance
valent :
![$\displaystyle \mathbb{E}[X] = \frac{n(1-p)}{p}$](img179.gif) et
et![$\displaystyle \quad
Var[X] = \frac{n(1-p)}{p^2}\;.
$](img180.gif)
On peut exprimer ![]() et
et ![]() en fonction de
en fonction de
![]() et
et ![]() .
.
![$\displaystyle n=\frac{(\mathbb{E}[X])^2}{Var[X]-\mathbb{E}[X]}$](img181.gif) et
et![$\displaystyle \quad
p=\frac{\mathbb{E}[X]}{Var[X]}\;.
$](img182.gif)
On en déduit deux
estimateurs convergents
de ![]() et
et ![]() en remplaçant
en remplaçant
![]() et
et ![]() par
leurs
estimateurs
par
leurs
estimateurs
![]() et
et ![]() dans ces expressions.
dans ces expressions.
L'inconvénient principal de la méthode des moments est que les estimateurs qu'elle fournit sont en général assez peu précis, et qu'il est difficile d'étudier leur loi autrement que par simulation.