Section : Recherche d'estimateurs
Précédent : Méthode des moments
Suivant : Estimateurs des moindres carrés

Estimation par ajustement

La modélisation probabiliste en statistique consiste à supposer qu'un échantillon observé $(x_1,\ldots,x_n)$ est une réalisation d'un échantillon théorique d'une certaine loi de probabilité $P_\theta$, où le paramètre $\theta$ est inconnu. Si tel était le cas, la distribution empirique $\widehat{P}$ de l'échantillon observé devrait être proche de $P_\theta$. La distribution empirique d'un échantillon est la loi de probabilité sur l'ensemble des valeurs, qui affecte chaque individu du poids 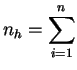$1/n$.

Définition 2.1   Soit $(x_1,\ldots,x_n)$ un échantillon observé, $c_1,\ldots,c_k$ les valeurs distinctes prises par les $x_i$ et pour $h=1,\ldots,k$ :

$$n_h = \sum_{i=1}^n$$   1$$_{c_h}(x_i)\;,$$

le nombre de fois où la valeur $c_h$ a été observée. La distribution empirique de l'échantillon est la loi de probabilité $\widehat{P}$ sur l'ensemble $\{c_1,\ldots,c_k\}$, telle que :

$$\widehat{P}(c_h) = \frac{n_h}{n}\;.$$

Parmi les moyens de quantifier l'ajustement d'une distribution empirique à une loi de probabilité théorique, nous en retiendrons deux : la distance du chi-deux (réservée aux lois discrètes) et la distance de Kolmogorov-Smirnov.

Définition 2.2   Soit $\{c_1,\ldots,c_r\}$ un ensemble fini fixé. Soit $P=(P(c_h))\,,\;h=1,\ldots,r$ une loi de probabilité sur cet ensemble, et $\widehat{P}=(\widehat{P}(c_h))\,,\;h=1,\ldots,r$ une distribution empirique sur cet ensemble. On appelle distance du chi-deux de $Q$ par rapport à $P$, et on note $D_{\chi^2}(P,\widehat{P})$, la quantité :

$$D_{\chi^2}(P,\widehat{P}) = \sum_{h=1}^r \frac{(P(c_h)-\widehat{P}(c_h))^2}{P(c_h)}\;.$$

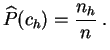
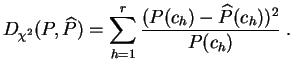
La distance de Kolmogorov-Smirnov est la distance de la norme uniforme entre fonctions de répartitions. Rappelons que la fonction de répartition empirique de l'échantillon $(x_1,\ldots,x_n)$ est la fonction de répartition de sa distribution empirique. C'est la fonction en escalier $\widehat{F}$ qui vaut 0 avant $x_{(1)}$, $i/n$ entre $x_{(i)}$ et $x_{(i+1)}$, et 1 après $x_{(n)}$ (les $x_{(i)}$ sont les statistiques d'ordre, c'est-à-dire les valeurs ordonnées de l'échantillon).

Définition 2.3   Soient $F$ la fonction de répartition d'une loi de probabilité et $\widehat{F}$ la fonction de répartition empirique de l'échantillon $(x_1,\ldots,x_n)$. On appelle distance de Kolmogorov-Smirnov de $F$ et $\widehat{F}$, et on note $D_{KS}(F,\widehat{F})$, la quantité :

$$D_{KS}(F,\widehat{F}) = \max_{i=1,\ldots,n}\, \Big\{\,\Big\vert ... ...i}{n}\Big\vert\,,\, \Big\vert F(x_{(i)})-\frac{i\!-\!1}{n}\Big\vert\,\Big\}\;.$$

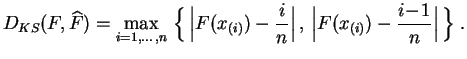
Etant donnés un échantillon et une famille de lois de probabilité $P_\theta$, dépendant du paramètre inconnu $\theta$, il est naturel de choisir comme modèle celle des lois de la famille qui s'ajuste le mieux aux données. Cela revient à donner comme estimation de $\theta$ celle pour laquelle la distance entre la loi théorique $P_\theta$ et la distribution empirique de l'échantillon est la plus faible.

Considérons par exemple un échantillon de données binaires. Notons $f$ la fréquence empirique des 1. La distance du chi-deux entre la loi de Bernoulli de paramètre $p$ et la distribution empirique est :

$$D_{\chi^2} = \frac{(f-p)^2}{p} + \frac{(1-f-1+p)^2}{1-p} = \frac{(f-p)^2}{p(1-p)}\;.$$

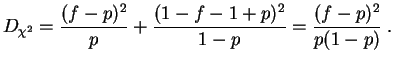
Cette distance est évidemment minimale pour $p=f$. Ceci s'étend trivialement à un nombre fini quelconque d'éventualités : la loi de probabilité qui ajuste le mieux une distribution empirique sur $c_1,\ldots,c_k$ au sens de la distance du chi-deux est celle qui charge chaque valeur $c_h$ avec une probabilité égale à la fréquence expérimentale de cette valeur.

En pratique, il est rare que l'on puisse ainsi calculer explicitement l'estimation d'un paramètre par ajustement. On doit alors procéder à une minimisation numérique sur le paramètre inconnu.

Section : Recherche d'estimateurs
Précédent : Méthode des moments
Suivant : Estimateurs des moindres carrés