Espérance

Rappelons l'interprétation d'une loi de probabilité comme une répartition de masse. L'espérance d'une loi de probabilité est le barycentre de cette répartition de masse.

Lois discrètes. Considérons une variable aléatoire discrète

, prenant les valeurs $\{x_k\,,\;k\in K\subset \mathbb{N}\}$ . Si la série $\displaystyle\sum\limits_{k\in K}\vert x_k\vert P[X=x_k]$ converge alors l'espérance $\mathbb{E}[X]$ est :

Soit

de densité

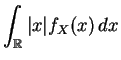sur $\mathbb{R}$ . Une densité s'interprète comme une distribution de masse continue sur $\mathbb{R}$ . C'est encore son barycentre que l'on calcule. Si l'intégrale $\displaystyle\int_{\mathbb{R}}\vert x\vert f_X(x)\,dx$ converge, alors l'espérance $\mathbb{E}[X]$ est :

Proposition 3.11

Si et admettent une espérance, alors :

$\displaystyle \forall a,b\in \mathbb{R}\,\,\mathbb{E}[aX+bY] =a\mathbb{E}[X] +b\mathbb{E}[Y] \;.$
Si et sont indépendantes et admettent une espérance alors :

$\displaystyle \mathbb{E}[XY] =\mathbb{E}[X] \, \mathbb{E}[Y] \;.$

Démonstration : La propriété 1 est une traduction de la linéarité de la somme (variables discrètes) ou de l'intégrale (variables continues). Nous démontrons la propriété 2 pour des variables discrètes.

prend les valeurs $(x_k)_{k\in K}$ ,

prend les valeurs $(y_h)_{h\in H}$ ,

étant indépendantes, le couple

prend les valeurs $(x_k,y_h)_{(h,k)\in K\times H}$ avec probabilité $P[X=x_k]\,P[Y=y_h]$ . On a donc :

$\displaystyle \mathbb{E}[X Y]$	$\displaystyle =$	$\displaystyle \sum_{(k,h)\in K\times H} x_k\,y_h\,P[X=x_k]\,P[Y=y_h]$
	$\displaystyle =$	$\displaystyle \displaystyle\sum\limits_{k\in K}x_kP[X=x_k]\, \displaystyle\sum\limits_{h\in H}y_hP[Y=y_h]$
	$\displaystyle =$	$\displaystyle \mathbb{E}[X]\,\mathbb{E}[Y]\;.$

Le terme d'espérance se justifie pleinement dans le cas d'un gain aléatoire. Voici l'exemple du Keno, pour

numéros cochés sur une grille (qui coûte

F).


Loi	Espérance

Uniforme ${\cal U}(\{1,\ldots,n\})$	$\frac{n+1}{2}$
Bernoulli ${\cal B}(1,p)$
Binomiale ${\cal B}(n,p)$
Géométrique ${\cal G}(p)$	$\frac{1}{p}$
Poisson ${\cal P}(\lambda)$	$\lambda$
Hypergéométrique ${\cal HG}(N,m,n)$	$n\frac{ m}{N}$
Binomiale négative ${\cal BN}(n,p)$	$\frac{n}{p}-n$

Uniforme ${\cal U}(a,b)$	$\frac{a+b}{2}$
Exponentielle ${\cal E}(\lambda )$	$\frac{1}{\lambda}$
Normale ${\cal N}(\mu,\sigma^2)$	$\mu$
Weibull ${\cal W}(a,\lambda)$	$\lambda^{-\frac{1}{a}} \Gamma(\frac{1}{a}+1)$
Gamma ${\cal G}(a,\lambda)$	$\frac{a}{\lambda}$
Chi-deux ${\cal X}^2(n)$
Béta ${\cal B}(a,b)$	$\frac{a}{a+b}$
Log-normale ${\cal LN}(\mu,\sigma^2)$	$e^{\mu+\sigma^2/2}$
Student ${\cal T}(n)$	0 si
Fisher ${\cal F}(n,m)$	$\frac{m}{m-2}$ si

On rencontre fréquemment le problème consistant à calculer l'espérance d'une variable aléatoire qui est fonction d'une autre variable variable aléatoire, dont la loi est connue : $\mathbb{E}[Y]=\mathbb{E}[\phi(X)]$ . Une première solution consiste à déterminer la loi de

, puis son espérance. La proposition suivante montre que ce n'est pas nécessaire.

Proposition 3.12 Soit $\phi$ une fonction de $\mathbb{R}$ dans $\mathbb{R}$ .

Soit une variable aléatoire discrète, prenant les valeurs $\{x_k\,,\;k\in K\subset \mathbb{N}\}$ . La variable aléatoire $\phi(X)$ admet une espérance si et seulement si la série
$\sum \vert\phi(x_k)\vert P[X=x_k]$ converge. Si c'est le cas, on a :

$\displaystyle \mathbb{E}[\phi(X)] = \sum_{k\in K} \phi(x_k)P[X=x_k]\;.$
Soit une variable aléatoire continue, de densité . La variable aléatoire $\phi(X)$ admet une espérance si et seulement si l'intégrale $\int \vert\phi(x)\vert f_X(x)\,dx$ converge. Si c'est le cas, on a :

$\displaystyle \mathbb{E}[\phi(X)] = \int_{\mathbb{R}} \phi(x)\,f_X(x)\,dx\;.$

Les calculs de variances du paragraphe suivant sont une application de cette proposition.

bon(s) numéro(s)	0	1	2	3	4
gain	0	0	0	100	1000
probabilité	0.2512	0.4275	0.2538	0.0622	0.0053

K	4	5	6	7	8	9	10
Espérance	11.50	10.41	11.82	11.25	11.78	11.19	11.62