![$\displaystyle P[A\,\vert\,B]=\frac{P[A\cap B]}{P[B]}
\;.
$](img54.gif)
La connaissance d'une information sur une expérience peut modifier l'idée qu'on se fait de la probabilité d'un évènement. La probabilité qu'il pleuve aujourd'hui est supérieure si le ciel est nuageux.
![$\displaystyle P[A\,\vert\,B]=\frac{P[A\cap B]}{P[B]}
\;.
$](img54.gif)
Interprétation :
Le fait de savoir que ![]() est réalisé réduit
l'ensemble des résultats possibles de
est réalisé réduit
l'ensemble des résultats possibles de ![]() à
à ![]() . A partir de là,
seules les éventualités de
. A partir de là,
seules les éventualités de ![]() ont une importance. La
probabilité
de
ont une importance. La
probabilité
de ![]() sachant
sachant ![]() doit donc être proportionnelle à
doit donc être proportionnelle à
![]() . Le
coefficient de proportionnalité
. Le
coefficient de proportionnalité ![]() assure que l'application qui à
assure que l'application qui à
![]() associe
associe ![]() est bien une
probabilité,
pour laquelle
est bien une
probabilité,
pour laquelle ![]() est
l'évènement certain.
est
l'évènement certain.
Point de vue fréquentiste :
Si on admet la
loi des grands nombres,
la
probabilité
doit être vue comme
une limite de
fréquences expérimentales.
Avec les notations du paragraphe
précédent,
![]() (resp.
(resp. ![]() ) est la
fréquence expérimentale
de
) est la
fréquence expérimentale
de ![]() (resp.
(resp. ![]() ), et on a :
), et on a :
![$\displaystyle P[A\,\vert\,B]=\frac{P[A\cap B]}{P[B]} \approx
\frac{n_{A\cap B}/n}{n_B/n}
=\frac{n_{A\cap B}}{n_B}
\;.
$](img60.gif)
Une loi de
probabilité conditionnelle
est une
loi de probabilité. En
particulier,
si ![]() et
et ![]() sont disjoints (incompatibles) alors :
sont disjoints (incompatibles) alors :
![$\displaystyle \begin{array}{rl}
P[A\cap B]= & P[A\,\vert\,B] \,P[B]
\\ [1ex]
= & P[B\,\vert\,A] \,P[A]
\;.
\end{array}$](img66.gif)
![$\displaystyle P[A]
=\sum_{i\in I}P[A\cap B_i]
=\sum_{i\in I}P[A\,\vert\,B] \,P[B_i]\;.
$](img68.gif)
![$\displaystyle P[B_j\,\vert\,A]
=\frac{P[B_j\cap A]}{P[A]}
=\frac{P[A\,\vert\,B_j] \,P[B_j]}{\sum\limits_{i\in I }P[A\,\vert\,B_i] \,P[B_i]}\;.
$](img70.gif)
L'idée intuitive d'indépendance
de deux évènements est la suivante :
![]() et
et ![]() sont
indépendants
si le fait de savoir que
sont
indépendants
si le fait de savoir que ![]() se produit ou
non ne modifie pas les chances
de
se produit ou
non ne modifie pas les chances
de ![]() . Ou encore : sur un
grand nombre d'expériences, la proportion des fois où
. Ou encore : sur un
grand nombre d'expériences, la proportion des fois où ![]() s'est
produit quand
s'est
produit quand ![]() était réalisé est approximativement la même
que quand il ne l'était pas.
était réalisé est approximativement la même
que quand il ne l'était pas.
Exemple :
![]() : "La bourse de New-York est en hausse".
: "La bourse de New-York est en hausse".
![]() : "Il pleut à Paris".
: "Il pleut à Paris".
Dire que ![]() et
et ![]() sont
indépendants,
c'est dire que la bourse
de New-York est en hausse aussi souvent quand il pleut à Paris
que quand il ne pleut pas.
sont
indépendants,
c'est dire que la bourse
de New-York est en hausse aussi souvent quand il pleut à Paris
que quand il ne pleut pas.
En terme de fréquences, on écrira :
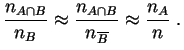
![$\displaystyle \frac{P[A\cap B]}{P[B]}=P[A]
\;.
$](img73.gif)
Attention.
Il ne faut pas confondre
indépendants
et incompatibles. Pour deux
évènements
incompatibles on a
![]() . Deux évènements incompatibles
de
probabilités
non nulles ne sont jamais
indépendants. Si l'un des
deux se produit, l'autre ne peut pas se produire.
. Deux évènements incompatibles
de
probabilités
non nulles ne sont jamais
indépendants. Si l'un des
deux se produit, l'autre ne peut pas se produire.
La définition d'indépendance se généralise de la façon suivante.
![$\displaystyle P[\bigcap_{j=1}^kA_{i_j}]
=\prod^k_{j=1}P[A_{i_j}]
\;.
$](img78.gif)
Dans les définitions que nous avons données jusqu'ici se trouve un cercle vicieux : Une probabilité est une limite de fréquences sur des expériences indépendantes . Deux évènements sont indépendants si la probabilité de leur intersection est le produit des probabilités.
Les deux notions de probabilité et d'indépendance sont donc indissociables, et en un sens impossibles à définir en pratique. Tout ce que l'on peut faire, c'est montrer la cohérence de leurs définitions. Une probabilité étant donnée pour les évènements observables à l'issue d'une expérience aléatoire, cette probabilité est bien limite de fréquences expérimentales quand la même expérience est répétée indépendamment. C'est la loi des grands nombres, que nous démontrerons plus loin. La question d'existence de "vraies" suites d'expériences indépendantes est beaucoup plus difficile. Nous l'aborderons, sans la résoudre, dans le chapitre suivant.