Section : Expériences Aléatoires
Précédent : Evènements
Suivant : Probabilités conditionnelles

Axiomes des Probabilités

Une loi de probabilité, ou distribution de probabilité, est une fonction $P$ qui à un évènement $A$ associe un nombre $P[A]$, sa probabilité. Ce nombre traduit les chances que l'évènement a de se produire. Le moyen le plus intuitif de définir une telle fonction est de répéter l'expérience aléatoire, et d'associer à tout évènement sa fréquence expérimentale. Si $n$ est le nombre d'expériences, $n_A$ le nombre de fois où l'évènement $A$ s'est produit, la fréquence expérimentale de $A$ est le rapport $n_A/n$. Voici par exemple $20$ répétitions d'une expérience dont les éventualités sont 0, 1 et 2.

$$0\,,\; 1\,,\; 1\,,\; 1\,,\; 0\,,\; 0\,,\; 1\,,\; 2\,,\; 1\,,\; 2\,,\; 0 \,,\; 1\,,\; 1\,,\; 2\,,\; 2\,,\; 0\,,\; 0\,,\; 0\,,\; 0\,,\; 2\;.$$

Dans cet exemple, la fréquence expérimentale de $\{0\}$ est $8/20$, celle de $\{1,2\}$ est $12/20$. L'inconvénient est que la fréquence expérimentale changera si on renouvelle les $n$ expériences. En d'autres termes l'ensemble des $n$ répétitions constitue une nouvelle expérience aléatoire . Cependant nous avons tous en tête une idée de la loi des grands nombres selon laquelle les fréquences expérimentales sur un grand nombre de répétitions varient peu. Voici quatre calculs successifs de la fréquence expérimentale de $\{0\}$, sur $20 \,000$ répétitions de la même expérience que ci-dessus.

$$0.3304\,,\;0.3273\,,\;0.3364\,,\;0.32415\;.$$

Les propriétés que l'on attend d'une probabilité sont celles des fréquences expérimentales. On les considère comme des axiomes de définition.

Ax1

Pour tout évènement $A$, $0\leq P[A]\leq 1$.

Ax2

La probabilité de l'évènement certain est 1 : $P[\Omega ]=1$.

Ax3

Si $(A_i)_{i\in\mathbb{N}}$ est une suite d'évènements disjoints deux à deux ($A_i$ et $A_j$ ne peuvent pas se produire en même temps si $i\neq j$), alors :

$$P[\bigcup\limits_{i\in\mathbb{N}}A_i] =\sum\limits_{i\in\mathbb{N}}P[A_i] \;.$$

Une conséquence immédiate des axiomes Ax2 et Ax3 est la relation entre les probabilités d'un évènement $A$ et de son complémentaire, noté $\overline A$.

$$P[\overline A] = 1 - P[A] \;.$$

Les lois de probabilité que l'on manipule en pratique sont de deux types.

1. Lois discrètes L'ensemble des éventualités $\Omega$ est fini ou dénombrable :
   $$\Omega = \{ \omega_i\,,\;i\in I\subset \mathbb{N}\}\;.$$
   Toutes les parties de $\Omega$ sont des évènements. Comme tout évènement est une réunion finie ou dénombrable de singletons, il suffit de définir la probabilité de chaque singleton  : pour tout $i\in I$,
   $$P[\{\omega_i\}] = p_i\;.$$
   Pour tout $A\subset \Omega$, la probabilité de $A$ sera alors déterminée par Ax3 :
   $$P[A] = \sum_{\omega_i\in A} P[\{\omega_i\}] = \sum_{\omega_i\in A} p_i\;.$$

   
   

   Exemple : Si l'ensemble des résultats est fini $\Omega =\{\omega _1, \ldots ,\omega _n\}$ et si aucune information ne permet de distinguer les résultats, il est naturel d'associer à chaque éventualité la probabilité $1/n$. La probabilité de tout évènement $A$ est alors Card$(A)/n$. Cette probabilité particulière s'appelle l'équiprobabilité. Tous les calculs dans ce cas se ramènent à des dénombrements :

       probabilité $$=\frac{\mbox{nombre de cas favorables} }{\mbox{nombre de cas possibles}}\;.$$

2. Lois continues L'ensemble des éventualités $\Omega$ est $\mathbb{R}$. Les évènements sont les intervalles, et tous les sous-ensembles de $\mathbb{R}$ que l'on peut former en combinant des intervalles par intersections et réunions. En théorie de la mesure, on les appelle des boréliens.
   Définition 1.1   On appelle densité de probabilité une fonction de $\mathbb{R}$ dans $\mathbb{R}^+$, continue par morceaux et d'intégrale 1.

   $$f(x)\geq 0\;,\;\forall x\in \mathbb{R}$$   et$$\quad \int_{\mathbb{R}} f(x)\,dx = 1\;.$$

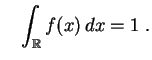
   Etant donnée une densité de probabilité, on définit une loi de probabilité sur $\mathbb{R}$ en associant à tout évènement l'intégrale de la densité sur cet évènement.

   $$P[A] = \int_{x\in A} f(x)\,dx\;.$$

   
   

   Exemple : Pour l'expérience aléatoire consistant à tirer au hasard un réel dans $[0,1]$ (appel de Random), on considèrera sur $\mathbb{R}$ la loi de probabilité continue, de densité :

   $$f(x) = \left\{ \begin{array}{ll} 1&\mbox{si } x\in [0 ,1]\;,\\ 0&\mbox{sinon.}\\ \end{array}\right.$$

Elle donne à tout intervalle inclus dans $[0,1]$ une probabilité égale à sa longueur.

Comme dans l'exemple ci-dessus, il est fréquent qu'une densité soit strictement positive sur un intervalle (éventuellement non borné) de $\mathbb{R}$, et nulle ailleurs. L'intervalle sur lequel $f$ est strictement positive s'appelle le support de la loi.

On peut voir une probabilité comme une répartition de masse sur l'ensemble des éventualités. La masse totale vaut 1. Dans le cas discret, elle est répartie sur chacune des éventualités en "grains de plomb" distincts. Dans le cas continu, elle est répartie sur tout un intervalle de $\mathbb{R}$, qui devient comme un fil de masse 1 dont la densité de masse serait variable. Calculer la probabilité d'un évènement, c'est calculer sa masse. A part cette analogie, quel sens pratique a la notion de probabilité ? Peut-on mesurer physiquement des probabilités ? Le seul sens concret que l'on puisse leur donner est celui, intuitif, de la loi des grands nombres. "Pile a une chance sur deux de se produire" signifie pour nous "Si je lance la pièce un grand nombre de fois, Pile sortira environ une fois sur deux."

Intuition : La probabilité d'un évènement est la limite de ses fréquences expérimentales sur un grand nombre d'expériences indépendantes.

Cette intuition comporte plusieurs coins d'ombres. Que les fréquences expérimentales convergent sous certaines hypothèses est un théorème (c'est ce théorème qui porte le nom de loi des grands nombres). Pourquoi rajouter l'adjectif "indépendantes" ?

Imaginez une machine de précision à lancer les pièces  : un bras articulé muni d'un plateau, relié à un ressort réglable à une valeur fixée une fois pour toutes. Mettons le ressort sous tension, posons la pièce sur le plateau, côté pile, et lâchons le ressort. Au premier essai on ne pourra pas prévoir si la pièce tombera sur pile ou face. Mais l'information apportée par le résultat du premier essai permettra de prévoir les suivants  : les expériences ne seront pas indépendantes. Les fréquences expérimentales vaudront 1 ou 0 mais ne fourniront aucun renseignement sur le fait que la pièce soit équilibrée ou non.

L'objectif principal du paragraphe suivant est de préciser les notions de dépendance et d'indépendance d'évènements et d'expériences aléatoires.

Section : Expériences Aléatoires
Précédent : Evènements
Suivant : Probabilités conditionnelles