Section : Simulation, modèles et réalité
Précédent : Simulation, modèles et réalité
Suivant : Générateurs pseudo-aléatoires

Modèles

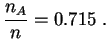
Nous donnons trois exemples d'expériences aléatoires qui nous permettront de cerner les rôles respectifs des mathématiques et de la simulation dans la modélisation d'expériences aléatoires.

Exemple 1 : Aiguille de Buffon.

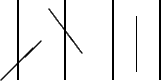
On lance au hasard une aiguille sur un parquet. On supposera pour simplifier que la longueur de l'aiguille est égale à la largeur d'une lame de parquet. Le problème consiste à calculer la probabilité pour que l'aiguille tombe à cheval sur 2 lames de parquet.

Une concrétisation de cette expérience se trouve au palais de la découverte : les "lames de parquet" sont métalliques, l'aiguille est retenue par un électro-aimant et tombe quand le visiteur appuie sur un interrupteur. Si elle tombe à cheval sur deux lames, il y a contact et un compteur est incrémenté. On peut donc calculer la fréquence expérimentale. Celle-ci est remarquablement proche de $2/\pi$ (des millions de visiteurs ont appuyé sur le bouton...). On a donc un moyen "expérimental" de calculer $\pi$. Notons que l'expérience du palais de la découverte est déjà une analogie, une idéalisation du problème initial : c'est un modèle physique.

Modèle mathématique.

Les hypothèses sont les suivantes.

• La position du milieu de l'aiguille est un réel au hasard entre 0 et $1/2$.
• L'angle de l'aiguille avec l'axe vertical est un réel au hasard entre 0 et $\pi/2$.
• Les choix de ces deux quantités sont des expériences indépendantes.

Comme conséquence du modèle mathématique, on peut démontrer que la probabilité cherchée vaut $2/\pi$.

Calcul par simulation

$n_A\leftarrow 0$
Répéter $n$ fois
$X \longleftarrow$ Random $/2$
$\theta \longleftarrow$ Random $*\pi/2$
Si $\cos(\theta) \geq 1-2X$ Alors $n_A \longleftarrow n_A+1$
finSi
finRépéter
$\overline X_n\leftarrow n_A/n$

Voici par exemple une fréquence empirique obtenue sur $n=10^6$ expériences.

$$\frac{n_A}{n}=0.636438\;,\; \frac{2n}{\overline n_A}=3.14249\;.$$

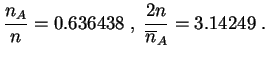
Dans les deux cas (calcul mathématique et simulation) on n'a fait que développer les conséquences des hypothèses de définition du modèle. La simulation n'a pas plus de rapport avec la réalité physique que le calcul mathématique. D'ailleurs, on est obligé d'introduire la valeur de $\pi$ dans l'algorithme pour au bout du compte...en déduire une estimation de cette valeur! Le miracle est que les conséquences calculées des hypothèses de modélisation puissent avoir un rapport avec une réalité physique, ou en d'autres termes que le modèle mathématique puisse être validé par confrontation avec l'expérience.

Exemple 2 : Paradoxe de Bertrand.
Dans un cercle de rayon 1, quelle est la probabilité pour qu'une corde choisie au hasard soit de longueur supérieure à $\sqrt{3}$ (qui est la longueur du coté du triangle équilatéral inscrit dans le cercle).

Modèle 1 : On choisit un point au hasard dans le disque et on lui associe la corde qui a ce point pour milieu. L'évènement est réalisé si le milieu est dans le disque concentrique de rayon $1/2$.

probabilité  : 1/4.

Modèle 2 : On choisit le milieu de la corde en tirant au hasard ses coordonnées polaires : $\rho$ réel au hasard entre 0 et 1, $\theta$ réel au hasard entre 0 et $2\pi$. L'évènement est réalisé si $\rho \leq 1/2$.

probabilité  : 1/2.

Modèle 3 : On choisit les deux extrémités de la corde au hasard sur le cercle.

probabilité  : 1/3.

Il n'y a rien de choquant au fait que des hypothèses de modélisation différentes conduisent à des conséquences différentes. On pourrait simuler chacun des modèles proposés et en déduire les différentes probabilités annoncées par le raisonnement. Aucun des modèles proposés n'est plus "vrai" qu'un autre, tant qu'aucune expérience physique n'est là pour valider les résultats.

Exemple 3 : Tour de cartes.
On attribue une valeur à chaque carte d'un jeu de $52$ cartes : 1 à $10$ et $10$ encore pour les valets, dames et rois. Les cartes sont étalées en ligne après avoir été mélangées.

Vous choisissez une carte parmi les $9$ premières et vous avancez vers la droite d'autant de cartes que la valeur de celle que vous aviez choisie. Vous recommencez jusqu'à ne plus pouvoir avancer (par exemple vous tombez sur un $6$ et il ne reste que $4$ cartes à sa droite). La dernière carte sur laquelle vous tombez est votre carte finale. Le magicien se propose de deviner quelle est votre carte finale, sans rien savoir de votre parcours. Pour cela, il choisit lui aussi une carte parmi les $9$ premières et itère le même algorithme. Il déclare ensuite que votre carte finale est la même que la sienne.

Si le jeu est mélangé au hasard, quelle probabilité le magicien a-t-il de deviner juste ? Je ne connais pas de réponse mathématique à cette question. S'il en existe une, elle est certainement très compliquée (le nombre de permutations de $52$ cartes, $52!$ a $68$ chiffres).

Quand un modèle est trop compliqué pour être traité mathématiquement le recours à la simulation s'impose. Voici une fréquence expérimentale obtenue sur la simulation de $10^6$ permutations aléatoires des $52$ cartes  :

$$\frac{n_A}{n} = 0.715\;.$$

Section : Simulation, modèles et réalité
Précédent : Simulation, modèles et réalité
Suivant : Générateurs pseudo-aléatoires