Section : Simulation, modèles et réalité
Précédent : Modèles
Suivant : Suites uniformes

Générateurs pseudo-aléatoires

Tous les langages (ou presque) disposent d'un générateur pseudo-aléatoire. Les syntaxes varient : ran, grand, rand, Random ... Ce sont des fonctions, qui au dire des manuels d'utilisation, "retournent des nombres au hasard". Ce que l'on entend par "nombres au hasard" dépend d'abord du type des nombres (booléens, entiers, réels). Nous conviendrons de noter Random la fonction qui "retourne un réel au hasard dans $[0,1]$". Ceci recouvre en fait deux propriétés distinctes, que nous admettrons comme postulats.

Postulats.

1. Pour tout $(a,b)$, $0\leq a<b\leq 1$, $P[$ Random $\in ]a,b] \,]=b-a$.
2. Les appels successifs de Random sont des expériences aléatoires indépendantes.

Interprétation.

Dans le langage courant "au hasard" ne signifie pas seulement aléatoire mais aussi uniformément réparti. Choisir au hasard, c'est donner les mêmes chances à tous les résultats possibles (équiprobabilité). On attend d'un réel "au hasard" dans $[0,1]$ qu'il tombe entre $0.4$ et $0.5$ avec probabilité $1/10$, de même qu'entre $0.8$ et $0.9$. Deux intervalles inclus dans $[0,1]$ ont la même probabilité d'être atteints s'ils ont même longueur, et cette probabilité est la longueur des intervalles. Les postulats ci-dessus ont une autre conséquence. Si on considère des couples successifs d'appels de Random comme des coordonnées de points du plan, ces points sont des "points au hasard" dans $[0,1]^2$. Le sens précis étant que ces points sont indépendants et :

$$\forall a, b\;,\; 0\leq a <b \leq 1\;,\; \forall c,d\;,\; 0\leq c<d \leq 1$$

$$P[$$ ( Random $_1$, Random $_2$)$$\in ]a,b]\times ]c,d] \,] =(b-a)(d-c) \;.$$

La probabilité qu'un point dont les deux coordonnées sont des appels de Random tombe dans un rectangle est la surface de ce rectangle. Ceci peut évidemment être étendu en dimension quelconque. Des triplets d'appels de Random successifs sont les coordonnées de "points au hasard" dans le cube en dimension 3, etc...

Proposition 2.1   Pour tout $k\in\mathbb{N}^*$, soient $(R_1,\ldots ,R_k)$ $k$ appels successifs de Random . Les postulats 1) et 2) entraînent que pour tout rectangle

$$D= ]a_1,b_1]\times\cdots\times ]a_k,b_k], \; 0\leq a_i<b_i\leq 1 \,, \;i=1,\ldots ,k \,,$$

$$P[ \,(R_1,\ldots ,R_k)\in D \,] =(b_1-a_1)\cdots (b_k-a_k) \;.$$

La probabilité pour Random de tomber sur n'importe quelle valeur particulière est nulle :

$$\forall a\in [0,1] \; P[ \,$$ Random $$=a \,]=0,$$

car

$$\forall \varepsilon >0\,,\; P[ \,$$ Random $$=a \,] \leq P[ \,$$ Random $$\in ]a-\varepsilon, \,a] \,] =\varepsilon \;.$$

En conséquence,

$$\begin{array}{rl} P[ \,\mbox{\tt Random }\in \, ]a,b] \,]= &... ... [1ex] = & P[ \,\mbox{\tt Random}\in ]a,b[ \,]\;. \end{array}$$

Il y a un paradoxe à admettre à la fois que Random peut prendre une infinité de valeurs distinctes et que la probabilité de tomber sur une valeur particulière est nulle. Nous verrons en pratique la situation est légèrement différente, sans que cela remette en cause les postulats de définition de Random.

Une fois admis les deux postulats, toute analyse d'algorithmes contenant Random est une démonstration mathématique qui ne doit contenir aucun à-peu-près.

Exemple 1 : (Int $(\,\cdot\,)$ désigne la partie entière).

$$X\longleftarrow ($$Int$$( \, \underbrace {\mbox{\tt Random} }_{R_1} * 3 \,))* (\mbox{Int}( \, \underbrace {\mbox{\tt Random}}_{R_2}* 2 \,))\;.$$

La variable aléatoire $X$ prend les valeurs 0, 1 ou 2.

$$P[X=2] = P[ ( \,R_1* 3 \,)=2 ( \,R_2* 2 \,)=1 \,]$$

$$= P[ \,R_1\in [2/3, \,1[ R_2\in[1/2, \,1[ \,]$$

$$= \left(1-\frac{2}{3}\right)\left(1-\frac{1}{2}\right)$$

$$= \frac{1}{6}\;.$$

On montre de même que $P[X=1]=1/6$ et $P[X=0]=4/6$.

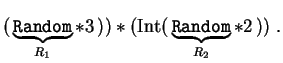
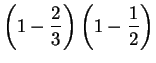Remarque : Contrairement aux apparences, l'algorithme ci-dessus ne retourne pas de valeurs entre $3$ et $6$. En théorie, la probabilité que Random retourne la valeur 1 est nulle. En pratique, les générateurs sont le plus souvent codés de manière à ne retourner ni 0 ni 1.

Exemple 2 : Lancer de dé.

$$D\longleftarrow$$   Int$$($$    Random $$*6 )+1$$

Pour tout $k\in \{1,\ldots , 6\}$,

$$P[D=k] = P[ * 6 \,)=k-1 \,]$$

$$= P[ * 6\in [k-1,k[ \,]$$

$$= P[ \in [(k-1)/6, \,k/6[ \,]$$

$$= \frac{k}{6}-\frac{k\!-\!1}{6}=\frac{1}{6}\;.$$

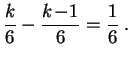Il ne faut pas déduire de cet exemple que Int $($ Random $*k)$ est la bonne manière de tirer un entier au hasard entre 0 et $k\!-\!1$. Les générateurs courants permettent différents types de sorties : réelles uniformes sur l'intervalle $[0,1]$, mais aussi booléennes, entières, et même complexes.

Les générateurs permettent de simuler des suites d'expériences aléatoires indépendantes, et donc de calculer de façon approchée des probabilités par application de la loi des grands nombres.

$n_A\leftarrow 0$
Répéter $n$ fois
expérience
Si $A$ réalisé alors $n_A\leftarrow n_A+1$
finSi
finRépéter
$f_A\leftarrow n_A/n\;.$

La variable $f_A$ est la fréquence expérimentale de l'évènement $A$ au cours des $n$ expériences.

Exemple :

$n_A\leftarrow 0$
Répéter $n$ fois
$D\leftarrow Int($ Random $* 6)+1$ (* Lancer d'un dé *)
Si $D\geq 4$ alors $n_A\leftarrow n_A+1$
finSi
finRépéter
$f_A\leftarrow n_A/n\;.$

En sortie de cet algorithme, $f_A$ contient un nombre d'autant plus proche de $0.5$ que $n$ est grand. Plus le nombre d'expériences est grand, plus précis est le résultat.

Section : Simulation, modèles et réalité
Précédent : Modèles
Suivant : Suites uniformes