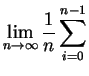 1
1
Au vu de la suite de réels retournée par un générateur particulier, comment décider que ce générateur convient ? Le seul moyen pratique d'estimer une probabilité est de l'exprimer comme une limite de fréquences expérimentales.
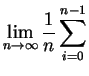 1
1
La notation
1![]() désigne la fonction indicatrice de l'ensemble
désigne la fonction indicatrice de l'ensemble ![]() .
.
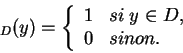
Le vecteur
![]() est le
est le ![]() -ème
-ème
![]() -uplet d'éléments consécutifs de la suite. La somme
-uplet d'éléments consécutifs de la suite. La somme
![]() 1
1![]() est le nombre de
est le nombre de ![]() -uplets d'éléments consécutifs de la suite qui
appartiennent à
-uplets d'éléments consécutifs de la suite qui
appartiennent à ![]() , parmi les
, parmi les ![]() premiers.
premiers.
La définition ci-dessus dit donc que parmi les ![]() -uplets d'éléments
consécutifs de la suite, la proportion de ceux qui tombent dans un
rectangle donné doit tendre vers le volume de ce rectangle (en dimension
-uplets d'éléments
consécutifs de la suite, la proportion de ceux qui tombent dans un
rectangle donné doit tendre vers le volume de ce rectangle (en dimension
![]() ). Cette définition est passablement utopique. En particulier elle
entraîne que la
probabilité
que
Random
tombe sur un point donné
est nulle. Comme qu'il n'y a qu'une
quantité dénombrable de rationnels dans
). Cette définition est passablement utopique. En particulier elle
entraîne que la
probabilité
que
Random
tombe sur un point donné
est nulle. Comme qu'il n'y a qu'une
quantité dénombrable de rationnels dans ![]() , la
probabilité
de
tomber sur un rationnel est également nulle. Or l'ordinateur ne
connaît que les décimaux, et même seulement un nombre fini d'entre
eux, donc la fonction
Random
ne peut retourner que des rationnels.
Qu'à cela ne tienne, si on sait construire une suite uniforme de
chiffres entre 0 et
, la
probabilité
de
tomber sur un rationnel est également nulle. Or l'ordinateur ne
connaît que les décimaux, et même seulement un nombre fini d'entre
eux, donc la fonction
Random
ne peut retourner que des rationnels.
Qu'à cela ne tienne, si on sait construire une suite uniforme de
chiffres entre 0 et ![]() , on pourra en déduire des réels
au hasard
dans
, on pourra en déduire des réels
au hasard
dans
![]() , approchés à la
, approchés à la ![]() -ème décimale, en considérant des
-ème décimale, en considérant des
![]() -uplets consécutifs de chiffres de la suite initiale. C'est le principe
des "tables de nombres au hasard" que l'on trouve encore dans certains
livres. La même remarque vaut bien sûr en base 2. Il suffirait donc de
savoir définir ce qu'est une suite de bits
au hasard.
Voici la définition de
-uplets consécutifs de chiffres de la suite initiale. C'est le principe
des "tables de nombres au hasard" que l'on trouve encore dans certains
livres. La même remarque vaut bien sûr en base 2. Il suffirait donc de
savoir définir ce qu'est une suite de bits
au hasard.
Voici la définition de ![]() -uniformité pour les suites de booléens.
-uniformité pour les suites de booléens.
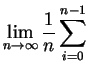 1
1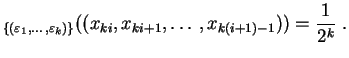
Ce que l'on attend en fait de la suite des appels de
Random
, c'est
qu'elle soit ![]() -uniforme, pour tout entier
-uniforme, pour tout entier ![]() (on dit
(on dit ![]() -uniforme).
C'est
évidemment illusoire, car l'infini n'existe pas pour un ordinateur. Tout ce
que l'on peut faire, c'est vérifier que rien d'invraisemblable ne se
produit pour la suite finie observée. C'est précisément l'objet des
tests statistiques
que de distinguer le plausible de ce qui est trop peu
vraisemblable, et des quantités de
tests
ont été imaginés pour mettre
les générateurs à l'épreuve.
-uniforme).
C'est
évidemment illusoire, car l'infini n'existe pas pour un ordinateur. Tout ce
que l'on peut faire, c'est vérifier que rien d'invraisemblable ne se
produit pour la suite finie observée. C'est précisément l'objet des
tests statistiques
que de distinguer le plausible de ce qui est trop peu
vraisemblable, et des quantités de
tests
ont été imaginés pour mettre
les générateurs à l'épreuve.
"Définition"
Un ![]() uplet de nombres dans
uplet de nombres dans ![]() sera dit pseudo-aléatoire s'il
passe avec succès une série de
tests statistiques,
chacun étant
destiné à vérifier une conséquence de la
sera dit pseudo-aléatoire s'il
passe avec succès une série de
tests statistiques,
chacun étant
destiné à vérifier une conséquence de la ![]() -uniformité. Le
nombre de ces
tests
ainsi que l'entier
-uniformité. Le
nombre de ces
tests
ainsi que l'entier ![]() sont fonction croissante de
l'exigence de l'utilisateur.
sont fonction croissante de
l'exigence de l'utilisateur.
Parmi les différentes formalisations du hasard qui ont pu être
proposées, la notion de suite ![]() -uniforme est la seule
utilisable en pratique : elle est la seule que l'on puisse tester pour
un générateur donné et elle suffit à justifier toutes les
applications des générateurs pseudo-aléatoires. Les
générateurs livrés avec les compilateurs courants sont issus
d'une longue expérimentation
statistique, et
n'ont survécu au
temps que parce qu'ils ont donné satisfaction à de nombreux
utilisateurs, ce qui n'empêche pas de rester vigilant.
-uniforme est la seule
utilisable en pratique : elle est la seule que l'on puisse tester pour
un générateur donné et elle suffit à justifier toutes les
applications des générateurs pseudo-aléatoires. Les
générateurs livrés avec les compilateurs courants sont issus
d'une longue expérimentation
statistique, et
n'ont survécu au
temps que parce qu'ils ont donné satisfaction à de nombreux
utilisateurs, ce qui n'empêche pas de rester vigilant.
Comment sont-ils programmés ? Même les suites récurrentes les plus
simples peuvent être chaotiques et donc constituer des exemples de
suites apparemment
aléatoires.
Et ce, même si le sens intuitif de
"aléatoire"
(impossible à prévoir) est contradictoire avec la
définition d'une suite récurrente (chaque terme fonction connue du
précédent). Pour un ordinateur, il n'existe qu'un nombre fini de
valeurs. Les valeurs de
Random
sont toujours calculées à
partir d'entiers répartis dans
![]() où
où ![]() est un grand nombre (de l'ordre
est un grand nombre (de l'ordre ![]() au moins pour les
générateurs usuels). Pour retourner un réel dans
au moins pour les
générateurs usuels). Pour retourner un réel dans ![]() , il
suffit de diviser par
, il
suffit de diviser par ![]() . En pratique, un nombre fini de valeurs
peuvent seules être atteintes, et elles le sont avec une
probabilité
positive. Ceci contredit les postulats de définition
de
Random
mais ne constitue pas un inconvénient majeur dans la
mesure où
. En pratique, un nombre fini de valeurs
peuvent seules être atteintes, et elles le sont avec une
probabilité
positive. Ceci contredit les postulats de définition
de
Random
mais ne constitue pas un inconvénient majeur dans la
mesure où ![]() est très grand. Pour obtenir un autre type de
réalisations, comme par exemple des entiers uniformes sur
est très grand. Pour obtenir un autre type de
réalisations, comme par exemple des entiers uniformes sur
![]() ou des booléens (pile ou face), passer par les
appels de
Random
est inutile, il vaut mieux partir du
générateur sur
ou des booléens (pile ou face), passer par les
appels de
Random
est inutile, il vaut mieux partir du
générateur sur
![]() sans diviser au préalable
par
sans diviser au préalable
par ![]() . Ceci est pris en compte par la plupart des langages courants.
. Ceci est pris en compte par la plupart des langages courants.
La valeur retournée par un générateur est une fonction de la valeur
précédente ou des
valeurs obtenues précédemment. Dans le premier cas la suite calculée
est une suite récurrente. Une "graine" ![]() étant choisie dans
étant choisie dans
![]() , les valeurs successives de la
suite sont définies par
, les valeurs successives de la
suite sont définies par
![]() , où
, où ![]() est une fonction de
est une fonction de
![]() dans lui-même, suffisamment simple pour être
calculée rapidement.
dans lui-même, suffisamment simple pour être
calculée rapidement.
On se heurte alors à un problème important : toute suite récurrente sur
un ensemble fini est périodique. La suite de valeurs retournée par
Random
bouclera forcément. Peut-on considérer comme
aléatoire
une
suite
périodique ? Oui peut-être, si la période est suffisamment élevée
par rapport au nombre de termes que l'on utilise. La prudence s'impose en
tout cas et il faut se méfier de l'idée intuitive que plus le passage de
![]() à
à ![]() sera compliqué, plus leurs valeurs seront
indépendantes
et meilleur sera le générateur.
sera compliqué, plus leurs valeurs seront
indépendantes
et meilleur sera le générateur.
Les générateurs les plus simples sont les générateurs par congruence. Ils sont de la forme suivante :
Divers résultats mathématiques permettent de justifier les "bons" choix
de ![]() ,
, ![]() et
et ![]() . Ils sont tombés en désuétude du fait de
l'apparition de nouveaux générateurs plus performants. Le générateur
suivant était très répandu et donnait en général satisfaction.
Il peut encore servir comme dépannage.
. Ils sont tombés en désuétude du fait de
l'apparition de nouveaux générateurs plus performants. Le générateur
suivant était très répandu et donnait en général satisfaction.
Il peut encore servir comme dépannage.
Tout générateur nécessite une initialisation. Pour une même valeur de
la graine ![]() , c'est la même suite de valeurs qui sera calculée à
chaque fois. Pour obtenir des résultats différents d'une exécution à
l'autre, il est nécessaire de changer la graine au début de chaque
exécution. Selon les langages, cette initialisation peut être laissée
au choix de l'utilisateur, ou être réalisée à partir du compteur de
temps (fonction randomize en Turbo Pascal, seed en C...).
L'instruction de randomisation doit figurer une seule
fois, en début de programme principal.
, c'est la même suite de valeurs qui sera calculée à
chaque fois. Pour obtenir des résultats différents d'une exécution à
l'autre, il est nécessaire de changer la graine au début de chaque
exécution. Selon les langages, cette initialisation peut être laissée
au choix de l'utilisateur, ou être réalisée à partir du compteur de
temps (fonction randomize en Turbo Pascal, seed en C...).
L'instruction de randomisation doit figurer une seule
fois, en début de programme principal.