La
fonction quantile
d'une
loi de probabilité
est l'inverse
(généralisé) de sa
fonction de répartition.
Si ![]() désigne la
fonction de répartition,
la
fonction quantile
désigne la
fonction de répartition,
la
fonction quantile
![]() est la fonction qui
à
est la fonction qui
à
![]() associe :
associe :
La fonction quantile empirique d'un échantillon est la fonction quantile de sa distribution empirique.
![$\displaystyle \forall u\in ]\frac{i-1}{n},\frac{i}{n}]\;,\quad
\widehat{Q}(u) = x_{(i)}\;.
$](img107.gif)
Pour certaines valeurs de ![]() , on donne un nom particulier aux
quantiles
, on donne un nom particulier aux
quantiles
![]() .
.
La médiane est une valeur centrale de l'échantillon : il y a autant de valeurs qui lui sont inférieures que supérieures. Si la distribution empirique de l'échantillon est peu dissymétrique, comme par exemple pour un échantillon simulé à partir d'une loi uniforme ou normale, la moyenne et la médiane sont proches. Si l'échantillon est dissymétrique, avec une distribution très étalée vers la droite, la médiane pourra être nettement plus petite que la moyenne. Contrairement à la moyenne, la médiane est insensible aux valeurs aberrantes. Elle possède une propriété d'optimalité par rapport à l'écart absolu moyen.
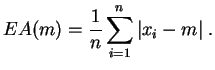
Cette fonction admet un minimum absolu en
![]() (la médiane).
La valeur de ce minimum est appelé écart absolu moyen.
(la médiane).
La valeur de ce minimum est appelé écart absolu moyen.
Démonstration :Le graphe de la fonction ![]() est constitué de segments de droites.
Sur l'intervalle
est constitué de segments de droites.
Sur l'intervalle
![]() , elle vaut :
, elle vaut :
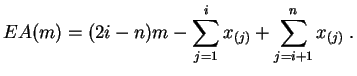
La pente
![]() est d'abord négative, puis positive. Si
est d'abord négative, puis positive. Si ![]() est impair
la
médiane
est impair
la
médiane
![]() est le seul minimum. Si
est le seul minimum. Si ![]() est pair, le minimum
est atteint sur tout un intervalle contenant
est pair, le minimum
est atteint sur tout un intervalle contenant
![]() , sur lequel la
pente s'annule.
, sur lequel la
pente s'annule.![]()
Il y a une part d'arbitraire dans la définition de la
fonction quantile
pour une distribution empirique : pour tous les points de l'intervalle
![]() la
fonction de répartition
vaut
la
fonction de répartition
vaut ![]() . Ce sont surtout
des raisons théoriques qui nous ont fait choisir
. Ce sont surtout
des raisons théoriques qui nous ont fait choisir ![]() plutôt que
n'importe quel autre de ces points comme valeur de
plutôt que
n'importe quel autre de ces points comme valeur de
![]() . Ce peut
être un assez mauvais choix en pratique. Considérons
l'échantillon
suivant, de taille 6.
. Ce peut
être un assez mauvais choix en pratique. Considérons
l'échantillon
suivant, de taille 6.
La
médiane
telle que nous l'avons définie vaut 3. Or comme valeur
centrale, le milieu de l'intervalle [3,7], à savoir 5, s'impose
clairement. Dans le cas
d'échantillons
de taille paire,
l'intervalle
![]() s'appelle l'intervalle médian,
et on définit parfois la
médiane
comme le milieu de l'intervalle
médian.
s'appelle l'intervalle médian,
et on définit parfois la
médiane
comme le milieu de l'intervalle
médian.
Ce problème ne se pose que dans le cas de petits
échantillons,
et pour les
quantiles
![]() pour lesquels
pour lesquels ![]() est de
la forme
est de
la forme ![]() (le plus souvent la médiane). Nous le négligerons
désormais et nous conserverons la définition 2.4.
(le plus souvent la médiane). Nous le négligerons
désormais et nous conserverons la définition 2.4.
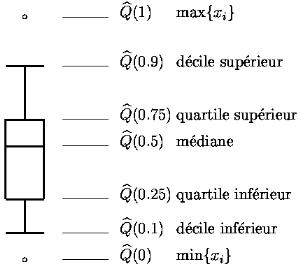
Même sur de très gros échantillons, les quantiles sont peu coûteux à calculer puisqu'il suffit de trier l'échantillon par ordre croissant pour calculer les statistiques d'ordre, et donc tous les quantiles simultanément. Ils fournissent une visualisation facile de la distribution empirique. Nous avons vu que la médiane est une valeur centrale. Pour mesurer la dispersion, on peut calculer l'étendue , qui est la différence entre la plus petite et la plus grande valeur. Mais cette étendue reflète plus les valeurs extrêmes que la localisation de la majorité des données. On appréhende mieux la dispersion d'un échantillon par les intervalles inter-quartiles et inter-déciles.
Ces intervalles sont à la base d'une représentation très compacte de la distribution empirique : le diagramme en boîte (ou boîte à moustaches, box plot, box-and-whisker plot). Il n'y a pas de définition standardisée de cette représentation. Elle consiste en une boîte rectangulaire, dont les deux extrémités sont les quartiles. Ces extrémités se prolongent par des traits terminés par des segments orthogonaux (les moustaches). La longueur de ces segments varie selon les auteurs. Nous proposons de la fixer aux déciles extrêmes. On représente aussi la médiane par un trait dans la boîte, et parfois les valeurs extrêmes par des points (voir figure ci-dessous).