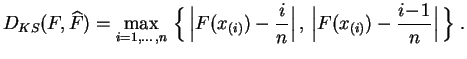Quand les
hypothèses
de
modélisation
conduisent à supposer que
![]() sont des réalisations de
variables indépendantes
et de
même loi, la
loi des grands nombres
justifie que l'on considère cette loi
comme proche de la
distribution empirique.
Toutes les caractéristiques
usuelles de la
distribution empirique
seront proches des caractéristiques
analogues de la loi théorique. On appelle problème
d'ajustement
le
problème consistant à trouver, parmi une famille de
lois de probabilité,
celle qui se rapproche le plus d'une
distribution empirique
observée sur un
échantillon.
Il est fréquent que l'on soit amené à effectuer une transformation des
données
avant
l'ajustement. Par exemple
dans les dosages médicaux, les lois
log-normales
apparaissent souvent. Une
variable aléatoire
suit une
loi log-normale
si
son logarithme suit une
loi normale.
Plutôt que d'ajuster directement avec
une
loi log-normale,
on commencera par transformer
l'échantillon
en
remplaçant les
données
par leurs logarithmes, et on ajustera le
nouvel
échantillon
par une
loi normale.
sont des réalisations de
variables indépendantes
et de
même loi, la
loi des grands nombres
justifie que l'on considère cette loi
comme proche de la
distribution empirique.
Toutes les caractéristiques
usuelles de la
distribution empirique
seront proches des caractéristiques
analogues de la loi théorique. On appelle problème
d'ajustement
le
problème consistant à trouver, parmi une famille de
lois de probabilité,
celle qui se rapproche le plus d'une
distribution empirique
observée sur un
échantillon.
Il est fréquent que l'on soit amené à effectuer une transformation des
données
avant
l'ajustement. Par exemple
dans les dosages médicaux, les lois
log-normales
apparaissent souvent. Une
variable aléatoire
suit une
loi log-normale
si
son logarithme suit une
loi normale.
Plutôt que d'ajuster directement avec
une
loi log-normale,
on commencera par transformer
l'échantillon
en
remplaçant les
données
par leurs logarithmes, et on ajustera le
nouvel
échantillon
par une
loi normale.
Nous nous contenterons dans un premier temps d'approches visuelles, nous introduirons ensuite des mesures quantitatives permettant d'évaluer des distances entre un modèle théorique et une distribution empirique.
Le cas le plus fréquent dans les applications est celui d'un échantillon
continu. La première approche consiste à superposer sur un même graphique
un
histogramme
des
données
avec la représentation graphique de la
densité
![]() de la loi théorique avec laquelle on souhaite les ajuster.
L'idée est la suivante. Au-dessus d'une classe
de la loi théorique avec laquelle on souhaite les ajuster.
L'idée est la suivante. Au-dessus d'une classe
![]() ,
l'histogramme
représente un rectangle de surface égale à la
fréquence expérimentale
de cette classe. Si
l'échantillon
était produit par
simulation
de la loi théorique, cette
fréquence expérimentale
serait
proche de la
probabilité
théorique, qui est l'intégrale de la
densité
sur la classe. Donc
l'histogramme
serait proche de la valeur
moyenne
de la
densité
sur la classe, à savoir :
,
l'histogramme
représente un rectangle de surface égale à la
fréquence expérimentale
de cette classe. Si
l'échantillon
était produit par
simulation
de la loi théorique, cette
fréquence expérimentale
serait
proche de la
probabilité
théorique, qui est l'intégrale de la
densité
sur la classe. Donc
l'histogramme
serait proche de la valeur
moyenne
de la
densité
sur la classe, à savoir :
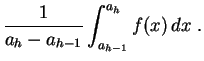
Un peu d'habitude permet de reconnaître à l'![]() il quand un histogramme
est trop éloigné d'une
densité
pour que
l'ajustement
soit bon.
il quand un histogramme
est trop éloigné d'une
densité
pour que
l'ajustement
soit bon.
L'inconvénient de
l'histogramme
est qu'il comporte une part importante
d'arbitraire dans le choix des classes. Une autre solution consiste à
superposer la
fonction de répartition
de la loi théorique avec
la
fonction de répartition empirique
![]() . La justification provient
encore de la
loi des grands nombres.
Au point
. La justification provient
encore de la
loi des grands nombres.
Au point ![]() , la fonction de
répartition empirique a pour valeur la proportion des
données
qui sont
inférieures à
, la fonction de
répartition empirique a pour valeur la proportion des
données
qui sont
inférieures à ![]() . Si les
données
avaient été simulées à
partir de la loi théorique, cette proportion devrait être proche de
la valeur correspondante de la
fonction de répartition théorique.
On préfère en général effectuer un changement d'axes qui donne
une représentation équivalente, mais plus facile à contrôler
visuellement : c'est
l'ajustement par quantiles
ou
QQ-plot
.
Désignons par
. Si les
données
avaient été simulées à
partir de la loi théorique, cette proportion devrait être proche de
la valeur correspondante de la
fonction de répartition théorique.
On préfère en général effectuer un changement d'axes qui donne
une représentation équivalente, mais plus facile à contrôler
visuellement : c'est
l'ajustement par quantiles
ou
QQ-plot
.
Désignons par ![]() la
fonction quantile
de la loi théorique.
Au lieu de représenter les points de coordonnées
la
fonction quantile
de la loi théorique.
Au lieu de représenter les points de coordonnées
![]() ,
pour la
fonction de répartition empirique,
le
QQ-plot
consiste à
représenter les points
,
pour la
fonction de répartition empirique,
le
QQ-plot
consiste à
représenter les points
![]() .
Si
l'ajustement
est correct, la
fonction quantile empirique
de
l'échantillon,
devrait être proche de la
fonction quantile théorique.
En particulier les points
.
Si
l'ajustement
est correct, la
fonction quantile empirique
de
l'échantillon,
devrait être proche de la
fonction quantile théorique.
En particulier les points
![]() seront proches de la première bissectrice, ce qui est très facile
à contrôler visuellement.
seront proches de la première bissectrice, ce qui est très facile
à contrôler visuellement.
Pour utiles qu'elles soient, les méthodes graphiques ne constituent pas une réponse mathématique au problème de l'ajustement. Pour quantifier l'éloignement de la distribution empirique par rapport à une loi théorique, on utilise des distances entre lois de probabilités. Nous introduisons deux de ces distances, la distance du chi-deux et la distance de Kolmogorov-Smirnov . La distance du chi-deux concerne uniquement les lois discrètes, mais on peut l'utiliser aussi pour des échantillons continus regroupés en classes.
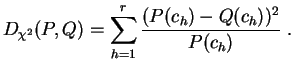
La "distance" du chi-deux
est donc une
moyenne
pondérée d'écarts
quadratiques entre les valeurs de ![]() et
et ![]() . Ce n'est pas une distance
au sens usuel du terme, puisqu'elle n'est même pas symétrique.
En pratique, on l'utilise toujours dans le cas où
. Ce n'est pas une distance
au sens usuel du terme, puisqu'elle n'est même pas symétrique.
En pratique, on l'utilise toujours dans le cas où
![]() est une distribution théorique et
est une distribution théorique et ![]() est la distribution empirique
est la distribution empirique
![]() .
.
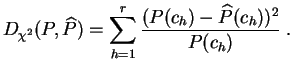
Pour un échantillon fixé, le meilleur ajustement sera celui pour lequel la distance du chi-deux est la plus faible.
L'autre notion de distance couramment utilisée pour les ajustements est la distance de Kolmogorov-Smirnov, qui est plus générale que la précédente. C'est la distance de la norme uniforme entre fonctions de répartitions.
En pratique, on utilise cette distance dans le cas où ![]() est la
fonction de répartition
de la loi théorique, et
est la
fonction de répartition
de la loi théorique, et
![]() est la
fonction de répartition empirique. Rappelons que la
fonction de répartition empirique
de
l'échantillon
est la
fonction de répartition empirique. Rappelons que la
fonction de répartition empirique
de
l'échantillon
![]() est la fonction en escalier qui
vaut 0 avant
est la fonction en escalier qui
vaut 0 avant ![]() ,
, ![]() entre
entre ![]() et
et ![]() , et
1 après
, et
1 après ![]() (les
(les ![]() sont les
statistiques d'ordre
de
l'échantillon). Toute
fonction de répartition
est croissante.
La
fonction de répartition empirique
étant constante
entre deux valeurs successives des
statistiques d'ordre,
il suffira
pour calculer la
distance de Kolmogorov-Smirnov,
d'évaluer la différence
entre
sont les
statistiques d'ordre
de
l'échantillon). Toute
fonction de répartition
est croissante.
La
fonction de répartition empirique
étant constante
entre deux valeurs successives des
statistiques d'ordre,
il suffira
pour calculer la
distance de Kolmogorov-Smirnov,
d'évaluer la différence
entre ![]() et
et
![]() aux points
aux points ![]() .
.