Reprenons encore le problème de tester l'effet d'un traitement
sur un
caractère
donné (le taux de cholestérol par
exemple). Un groupe témoin sans traitement correspond à un premier
échantillon
![]() de la loi
de la loi ![]() . Sur un deuxième
groupe, avec traitement, les valeurs mesurées sont celles de
l'échantillon
. Sur un deuxième
groupe, avec traitement, les valeurs mesurées sont celles de
l'échantillon
![]() de la loi
de la loi ![]() . Les deux lois
. Les deux lois ![]() et
et ![]() sont
inconnues. Si le traitement n'a aucun effet
(hypothèse nulle),
les deux lois sont identiques.
sont
inconnues. Si le traitement n'a aucun effet
(hypothèse nulle),
les deux lois sont identiques.
L'idée du
test de Wilcoxon
est la suivante : si on rassemble
les deux
échantillons,
et que l'on range les valeurs dans l'ordre, l'alternance des ![]() et
des
et
des ![]() devrait être
assez régulière. On aura des doutes sur
devrait être
assez régulière. On aura des doutes sur
![]() si les
si les ![]() sont
plutôt plus grands que les
sont
plutôt plus grands que les ![]() , ou plus petits, ou plus fréquents
dans une certaine plage de valeurs. On commence donc par écrire
les
statistiques d'ordre
de
l'échantillon
global (s'il y a des ex-æquo,
on tire
au hasard
une permutation). On obtient ainsi une suite
mélangée des
, ou plus petits, ou plus fréquents
dans une certaine plage de valeurs. On commence donc par écrire
les
statistiques d'ordre
de
l'échantillon
global (s'il y a des ex-æquo,
on tire
au hasard
une permutation). On obtient ainsi une suite
mélangée des ![]() et des
et des ![]() . On calcule ensuite la somme
des rangs des
. On calcule ensuite la somme
des rangs des ![]() , notée
, notée ![]() (c'est la
statistique
de
Wilcoxon
). Sous
l'hypothèse
(c'est la
statistique
de
Wilcoxon
). Sous
l'hypothèse
![]() , la loi de
, la loi de ![]() se
calcule facilement : sur un
échantillon
de taille
se
calcule facilement : sur un
échantillon
de taille
![]() , il y a
, il y a
![]() ordres possibles.
Le nombre de rangements possibles des
ordres possibles.
Le nombre de rangements possibles des ![]() est
est
![]() , et
ils sont
équiprobables.
On a donc pour tout
, et
ils sont
équiprobables.
On a donc pour tout
![]() entier allant de
entier allant de
![]() à
à
![]() :
:
![$\displaystyle \mathbb{P}_{{\cal H}_0}[\,W_x = m\,] =
\frac{k_m}{\binom{n_x+n_y}{n_x}}\;,
$](img205.gif)
Il est facile de tabuler numériquement la loi de ![]() , pour des valeurs
raisonnables de
, pour des valeurs
raisonnables de ![]() et
et ![]() . Pour les grandes valeurs, on
dispose du résultat d'approximation normale suivant :
. Pour les grandes valeurs, on
dispose du résultat d'approximation normale suivant :
Voici par exemple deux échantillons de taille 10.
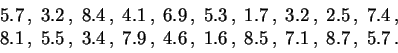
Voici les
statistiques d'ordre
de
l'échantillon
de taille
20 regroupé (les valeurs ![]() du premier
échantillon
sont soulignées).
du premier
échantillon
sont soulignées).
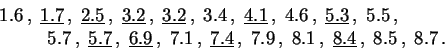
La
statistique
![]() prend la valeur :
prend la valeur :
Les valeurs du premier
échantillon
ont tendance à être plus petites
que celles du second. On cherche à savoir si cette tendance
est significative, on réalisera donc un
test unilatéral
à gauche
(rejet d'une valeur trop petite de ![]() ).
La
p-valeur
correspondante est :
).
La
p-valeur
correspondante est :
Le
test de Mann-Whitney
provient d'une autre approche mais il est équivalent
au précédent. Dans l'exemple ci-dessus, nous voulions vérifier
que les valeurs du premier
échantillon
étaient plus souvent plus
petites que celles du second. On aurait pu pour cela compter le
nombre de couples ![]() pour lesquels
pour lesquels
![]() (avec choix
aléatoire
en cas d'ex-æquo).
(avec choix
aléatoire
en cas d'ex-æquo).
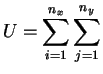 1
1
On vérifie aisément que les deux
statistiques
![]() et
et ![]() sont liées
par la relation suivante :
sont liées
par la relation suivante :