Nous considérons dans ce paragraphe le problème de tester l'indépendance
de deux
caractères
binaires, indicateurs de deux évènements distincts.
C'est un cas que l'on rencontre en médecine,
chaque fois qu'est posé le problème d'une détection
thérapeutique. Appelons ![]() (pour maladie) le premier évènement,
et
(pour maladie) le premier évènement,
et ![]() (pour symptôme) le second. Le symptôme peut être un taux
élevé d'une certaine substance ou la réaction positive à un
test
de dépistage, comme un alcootest. Sur chaque
individu
d'une
population
de taille
(pour symptôme) le second. Le symptôme peut être un taux
élevé d'une certaine substance ou la réaction positive à un
test
de dépistage, comme un alcootest. Sur chaque
individu
d'une
population
de taille ![]() , on a observé la présence ou l'absence de
la maladie et du symptôme. On dispose donc des
, on a observé la présence ou l'absence de
la maladie et du symptôme. On dispose donc des ![]() résultats suivants.
résultats suivants.
L'hypothèse nulle est :
Le
test du chi-deux de contingence,
vu au paragraphe précédent est un des moyens
de tester
![]() . Il
présente l'inconvénient de ne pas distinguer une tendance
positive (le symptôme est en faveur de la maladie) d'une
dépendance négative.
On utilise aussi le
rapport de cotes
(odds-ratio en anglais). La
cote (au sens des parieurs) d'un évènement est le rapport de
la
probabilité
de l'évènement à celle de son complémentaire.
La cote de la maladie peut se calculer parmi les individus ayant le
symptôme (
. Il
présente l'inconvénient de ne pas distinguer une tendance
positive (le symptôme est en faveur de la maladie) d'une
dépendance négative.
On utilise aussi le
rapport de cotes
(odds-ratio en anglais). La
cote (au sens des parieurs) d'un évènement est le rapport de
la
probabilité
de l'évènement à celle de son complémentaire.
La cote de la maladie peut se calculer parmi les individus ayant le
symptôme (
![]() ) et parmi ceux qui ne l'ont
pas (
) et parmi ceux qui ne l'ont
pas (
![]() ). Le
rapport de cotes
théorique est le quotient de ces deux quantités.
). Le
rapport de cotes
théorique est le quotient de ces deux quantités.
![$\displaystyle RC = \frac{P[M\,\vert\,S]/P[\overline{M}\,\vert\,S]}{
P[M\,\vert\...
...overline{M}\cap\overline{S}]}{
P[\overline{M}\cap S]\,P[M\cap\overline{S}]}\;.
$](img180.gif)
Le rapport de cotes vaut1 si la maladie et le symptôme sont indépendants, il est supérieur à1 si le symptôme est en faveur de la maladie. Quand des observations ont été menées sur un échantillon, on peut approcher les probabilités théoriques par des fréquences expérimentales. Ceci conduit à la définition du rapport de cotes empirique.
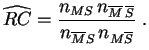
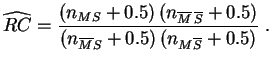
Exemple : Reprenons les données du paragraphe précédent.
La cote (empirique) des névroses parmi les individus ayant des tendances suicidaires est :
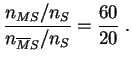
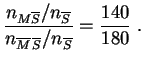
Le rapport de cotes empirique vaut :
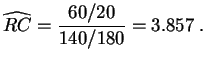
Il y a une dépendance positive entre les tendances suicidaires et
les névroses. La question est de savoir si
cette dépendance est significative. Il est difficile d'expliciter
la
loi de probabilité
du
rapport de cotes
sous l'hypothèse
![]() , autrement que par
simulation.
Pour de grands
échantillons,
on utilise le résultat asymptotique suivant.
, autrement que par
simulation.
Pour de grands
échantillons,
on utilise le résultat asymptotique suivant.
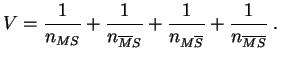
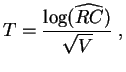
Dans notre exemple, la
statistique
![]() prend la valeur
prend la valeur
![]() . Sa
p-valeur
est :
. Sa
p-valeur
est :