Le
test du chi-deux
concerne uniquement les
lois discrètes,
mais on peut
l'utiliser aussi pour des
échantillons
continus regroupés en classes.
Le
modèle
de base est toujours un
échantillon
![]() d'une loi inconnue. Les classes, notées
d'une loi inconnue. Les classes, notées
![]() sont
une partition de l'ensemble des valeurs possibles.
L'hypothèse
à tester
porte sur les
probabilités
des classes, pour lesquelles on se donne
des valeurs théoriques
sont
une partition de l'ensemble des valeurs possibles.
L'hypothèse
à tester
porte sur les
probabilités
des classes, pour lesquelles on se donne
des valeurs théoriques
![]() .
.
Sous
l'hypothèse
![]() , la
distribution empirique
de l'échantillon
sur les classes doit être proche de la distribution théorique.
La
distribution empirique
est celle des
fréquences
de
l'échantillon
dans
les classes.
, la
distribution empirique
de l'échantillon
sur les classes doit être proche de la distribution théorique.
La
distribution empirique
est celle des
fréquences
de
l'échantillon
dans
les classes.
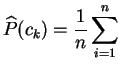 1
1On mesure l'adéquation de la distribution empirique à la distribution théorique par la distance du chi-deux.
La ``distance'' du
chi-deux
est donc une moyenne
pondérée d'écarts
quadratiques entre les valeurs de ![]() et
et
![]() . Ce n'est pas une
distance au sens usuel du terme, puisqu'elle n'est même pas symétrique.
. Ce n'est pas une
distance au sens usuel du terme, puisqu'elle n'est même pas symétrique.
La
loi de probabilité
de
![]() n'a pas d'expression
explicite en général. On utilise le résultat suivant.
n'a pas d'expression
explicite en général. On utilise le résultat suivant.
Si
l'hypothèse
![]() est fausse, alors la variable
est fausse, alors la variable
![]() tend vers l'infini. C'est donc un test
unilatéral
à droite que l'on appliquera (rejet des trop grandes
valeurs).
tend vers l'infini. C'est donc un test
unilatéral
à droite que l'on appliquera (rejet des trop grandes
valeurs).
L'exemple classique d'application du test est l'expérience de Mendel. Chez les pois, le caractère couleur est codé par un gène présentant deux formes allèles C et c, correspondant aux couleurs jaune et vert. Le jaune est dominant, le vert récessif. La forme, rond ou ridé, est portée par un autre gène à deux allèles R (dominant) et r (récessif). Si on croise deux individus dont le génotype est CcRr, on peut obtenir 16 génotypes équiprobables. Les descendants seront jaunes et ronds dans 9 cas sur 16, jaunes et ridés dans 3 cas sur 16, verts et ronds dans 3 cas sur 16, verts et ridés dans 1 cas sur 16. Dans ses expériences, Mendel a obtenu les résultats suivants.
La valeur prise par la
statistique
![]() est 0.47.
D'après le théorème 2.4, la région de rejet
doit être calculée par référence à la
loi du chi-deux
est 0.47.
D'après le théorème 2.4, la région de rejet
doit être calculée par référence à la
loi du chi-deux
![]() . Par exemple,
au
seuil
0.05, on devrait rejeter les valeurs supérieures à
. Par exemple,
au
seuil
0.05, on devrait rejeter les valeurs supérieures à
![]() 7.81. La
p-valeur
de 0.47 est
7.81. La
p-valeur
de 0.47 est
![]() 0.925. Le résultat est donc tout à fait
compatible avec
0.925. Le résultat est donc tout à fait
compatible avec
![]() , et même un peu trop : nombreux
sont ceux qui pensent que Mendel a pu arranger les résultats pour qu'ils
coïncident aussi bien avec sa théorie !
, et même un peu trop : nombreux
sont ceux qui pensent que Mendel a pu arranger les résultats pour qu'ils
coïncident aussi bien avec sa théorie !
L'exemple suivant concerne 10000 familles de 4 enfants pour lesquelles
on connaît le nombre de garçons, entre 0 et 4. Le modèle
le plus simple qu'on puisse proposer est que les naissances
sont
indépendantes,
les deux sexes étant
équiprobables.
L'hypothèse nulle
est donc que la loi du nombre de garçons
pour une famille de 4 enfants suit la
loi binomiale
![]() .
Les
fréquences
observées et théoriques sont les suivantes :
.
Les
fréquences
observées et théoriques sont les suivantes :
La valeur prise par la
statistique
![]() est 34.47.
D'après le théorème 2.4, la région de rejet
doit être calculée par référence à la
loi du chi-deux
de paramètre 5-1=4. Par exemple,
au
seuil
0.05, on devrait rejeter les valeurs supérieures à
est 34.47.
D'après le théorème 2.4, la région de rejet
doit être calculée par référence à la
loi du chi-deux
de paramètre 5-1=4. Par exemple,
au
seuil
0.05, on devrait rejeter les valeurs supérieures à
![]() . La
p-valeur
de 34.47 est
. La
p-valeur
de 34.47 est
![]() . On peut donc rejeter
l'hypothèse
. On peut donc rejeter
l'hypothèse
![]() .
.
Le théorème 2.4 n'est qu'un résultat asymptotique.
On ne peut l'utiliser que pour des tailles
d'échantillons
au moins de
l'ordre de la centaine. De plus l'approximation qu'il décrit est
d'autant moins bonne que les
probabilités
des classes sont faibles.
Comme règle empirique, on impose parfois que l'effectif théorique
![]() de chaque classe soit au moins égal à 5. Pour atteindre
cet objectif, on peut être amené à effectuer des regroupements
de classes, consistant à former une nouvelle classe par la réunion
de plusieurs anciennes. Les
fréquences
empiriques et les
probabilités
théoriques s'ajoutent alors.
de chaque classe soit au moins égal à 5. Pour atteindre
cet objectif, on peut être amené à effectuer des regroupements
de classes, consistant à former une nouvelle classe par la réunion
de plusieurs anciennes. Les
fréquences
empiriques et les
probabilités
théoriques s'ajoutent alors.
Le
test du chi-deux
est souvent utilisé pour tester l'ajustement
à une famille particulière dépendant d'un paramètre. Dans ce
cas, on est amené à estimer le paramètre à partir des
données.
Le théorème 2.4 n'est alors plus tout à fait valable.
Si on a estimé ![]() paramètres par la méthode du
maximum de vraisemblance,
à partir des
fréquences
des différentes classes,
on doit remplacer la loi
paramètres par la méthode du
maximum de vraisemblance,
à partir des
fréquences
des différentes classes,
on doit remplacer la loi
![]() par
la loi
par
la loi
![]() .
.
Reprenons l'exemple du nombre de garçons dans les familles de 4 enfants, mais pour tester cette fois-ci l'hypothèse nulle :
Le paramètre
On applique alors le
test,
mais avec une distribution théorique
calculée en tenant compte de la valeur estimée du paramètre :
la loi
![]() .
.
La valeur prise par la
statistique
![]() est
maintenant 0.9883. Elle doit être comparée aux valeurs
de la
loi du chi-deux
de paramètre 5-1-1=3.
La
p-valeur
de 0.9883 est
est
maintenant 0.9883. Elle doit être comparée aux valeurs
de la
loi du chi-deux
de paramètre 5-1-1=3.
La
p-valeur
de 0.9883 est
![]() ,
ce qui montre que le résultat est tout à fait compatible avec
l'hypothèse
,
ce qui montre que le résultat est tout à fait compatible avec
l'hypothèse
![]() . En conclusion, on peut accepter
l'idée que les naissances sont
indépendantes,
mais la proportion
de garçons est significativement supérieure à 0.5.
. En conclusion, on peut accepter
l'idée que les naissances sont
indépendantes,
mais la proportion
de garçons est significativement supérieure à 0.5.
On est souvent amené à estimer des paramètres à partir
des
données
non groupées, ou par une autre méthode que le
maximum de vraisemblance.
Dans ce cas, on ne dispose pas de résultat théorique clair.
La valeur limite à partir de laquelle on devra rejeter l'hypothèse
![]() au
seuil
au
seuil
![]() est comprise entre
est comprise entre
![]() et
et
![]() .
En pratique, après avoir calculé la valeur
.
En pratique, après avoir calculé la valeur ![]() prise par
prise par
![]() en tenant compte de
en tenant compte de ![]() paramètres
estimés, une attitude prudente consistera à :
paramètres
estimés, une attitude prudente consistera à :
Un cas particulier du
test du chi-deux
permet de tester l'indépendance
de deux
caractères
statistiques.
Il porte le nom de
chi-deux de contingence.
Les deux
caractères,
mesurés sur une même
population,
sont ![]() et
et ![]() , la taille de
l'échantillon
est
, la taille de
l'échantillon
est ![]() . Les
modalités ou classes de
. Les
modalités ou classes de ![]() seront notées
seront notées
![]() , celles de
, celles de ![]() sont notées
sont notées
![]() . On note :
. On note :
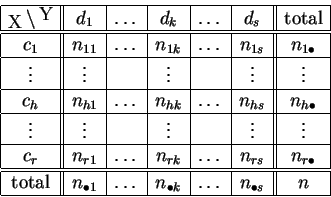
Chaque ligne et chaque colonne correspond à un sous-échantillon
particulier. La ligne d'indice ![]() est la répartition sur
est la répartition sur
![]() des individus pour lesquels le
caractère
des individus pour lesquels le
caractère
![]() prend la valeur
prend la valeur ![]() .
La colonne d'indice
.
La colonne d'indice ![]() est la répartition sur
est la répartition sur
![]() des individus pour lesquels le
caractère
des individus pour lesquels le
caractère
![]() prend la valeur
prend la valeur ![]() . En
divisant les lignes et les colonnes par leurs sommes, on obtient sur chacune
des
distributions empiriques
constituées de
fréquences
conditionnelles.
Pour
. En
divisant les lignes et les colonnes par leurs sommes, on obtient sur chacune
des
distributions empiriques
constituées de
fréquences
conditionnelles.
Pour
![]() et
et
![]() , on les notera :
, on les notera :
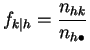 et
et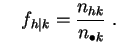
Ces distributions empiriques conditionnelles s'appellent les profils-lignes et profils-colonnes.
Pour le
modèle probabiliste,
les observations proviennent d'un
échantillon
![]() d'une loi bidimensionnelle.
L'hypothèse
à tester est que les deux
marginales
de cette loi
sont
indépendantes.
Si c'est
le cas, les profils-lignes seront tous peu différents de la distribution
empirique de
d'une loi bidimensionnelle.
L'hypothèse
à tester est que les deux
marginales
de cette loi
sont
indépendantes.
Si c'est
le cas, les profils-lignes seront tous peu différents de la distribution
empirique de ![]() , et les profils-colonnes de celle de
, et les profils-colonnes de celle de ![]() :
:
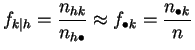 et
et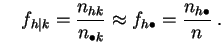
C'est équivalent à dire que les fréquences conjointes doivent être proches des produits de fréquences marginales.
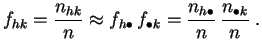
Les
fréquences
conjointes d'une part (distribution observée), et les
produits de fréquences
marginales
d'autre part (distribution théorique),
constituent deux distributions de probabilité
sur l'ensemble produit
![]() .
On peut donc calculer la distance
du
chi-deux
de l'une par rapport à l'autre.
.
On peut donc calculer la distance
du
chi-deux
de l'une par rapport à l'autre.
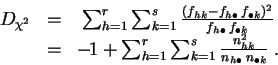
Démonstration : La première expression est l'application directe de la définition 2.3. Pour passer à la seconde, on développe le carré.
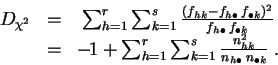
![]()
D'après ce qui a été dit précédemment, pour ![]() assez grand,
on peut approcher la loi de
assez grand,
on peut approcher la loi de
![]() par une
loi du chi-deux,
dont le paramètre est le nombre de classes
moins 1, diminué du nombre de paramètres estimés à partir
des
données
groupées en classes. Ici, ce sont les fréquences
marginales
qui ont été estimées. Il y en a
par une
loi du chi-deux,
dont le paramètre est le nombre de classes
moins 1, diminué du nombre de paramètres estimés à partir
des
données
groupées en classes. Ici, ce sont les fréquences
marginales
qui ont été estimées. Il y en a ![]() pour le
caractère
pour le
caractère
![]() , et
, et ![]() pour le
caractère
pour le
caractère
![]() (la dernière
est le complément à 1 de la somme des autres). Le paramètre de la
loi du chi-deux
sera donc :
(la dernière
est le complément à 1 de la somme des autres). Le paramètre de la
loi du chi-deux
sera donc :
Voici un exemple de deux
caractères
binaires, concernant des malades,
pour lesquels on a observé s'il ont ou non une tendance
suicidaire (caractère ![]() ). Leurs maladies ont été classées en
``psychoses'' et ``névroses'' (caractère Y). On souhaite savoir
s'il y a une dépendance entre les tendances suicidaires et le classement
des malades. Supposons que la
table de contingence
observée soit :
). Leurs maladies ont été classées en
``psychoses'' et ``névroses'' (caractère Y). On souhaite savoir
s'il y a une dépendance entre les tendances suicidaires et le classement
des malades. Supposons que la
table de contingence
observée soit :
La distance du
chi-deux de contingence,
calculée à partir de cette
table est 0.0708. La valeur prise par la
statistique
![]() est 28.33, que l'on doit comparer à la loi
est 28.33, que l'on doit comparer à la loi
![]() . La
p-valeur
est de :
. La
p-valeur
est de :