Le
test de Kolmogorov-Smirnov
est un
test d'ajustement
à une loi
continue, qui prend en compte l'ensemble des
quantiles,
contrairement au
test
local du paragraphe précédent. Le modèle
est encore un
échantillon
![]() d'une loi inconnue
d'une loi inconnue ![]() .
L'hypothèse nulle
est :
.
L'hypothèse nulle
est :
L'idée est la suivante : si
l'hypothèse
![]() est correcte, alors
la
fonction de répartition empirique
est correcte, alors
la
fonction de répartition empirique
![]() de
l'échantillon
doit être proche de
de
l'échantillon
doit être proche de ![]() . La
fonction de répartition empirique
est
la fonction de
. La
fonction de répartition empirique
est
la fonction de
![]() dans [0,1], qui vaut :
dans [0,1], qui vaut :
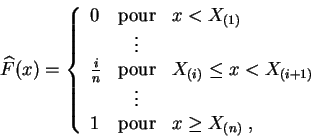
où les ![]() sont les
statistiques d'ordre
de l'échantillon
(valeurs de
l'échantillon
rangées par ordre croissant).
En d'autres termes,
sont les
statistiques d'ordre
de l'échantillon
(valeurs de
l'échantillon
rangées par ordre croissant).
En d'autres termes,
![]() est la proportion d'éléments de
l'échantillon
qui sont inférieurs ou égaux à
est la proportion d'éléments de
l'échantillon
qui sont inférieurs ou égaux à ![]() .
.
On mesure l'adéquation de la
fonction de répartition empirique
à
la fonction ![]() par la
distance de Kolmogorov-Smirnov,
qui est la distance de la norme uniforme entre fonctions de répartitions.
Pour la calculer, il suffit d'évaluer la différence
entre
par la
distance de Kolmogorov-Smirnov,
qui est la distance de la norme uniforme entre fonctions de répartitions.
Pour la calculer, il suffit d'évaluer la différence
entre
![]() et
et ![]() aux points
aux points ![]() .
.

Sous
l'hypothèse
![]() , la loi de la
statistique
, la loi de la
statistique
![]() ne dépend pas de
ne dépend pas de ![]() , car les images de
, car les images de ![]() par
par ![]() sont des
variables aléatoires
de loi
sont des
variables aléatoires
de loi
![]() .
Mais la
fonction de répartition
de
.
Mais la
fonction de répartition
de
![]() n'a
pas d'expression explicite simple et doit être calculée numériquement.
Pour des
échantillons
de taille suffisante,
on utilise le résultat asymptotique suivant :
n'a
pas d'expression explicite simple et doit être calculée numériquement.
Pour des
échantillons
de taille suffisante,
on utilise le résultat asymptotique suivant :
La série converge très rapidement. En pratique, pour t>0.56, la somme des trois premiers termes donne déjà une approximation avec une erreur inférieure à 10-4.
Si
l'hypothèse
![]() est fausse,
est fausse,
![]() tend vers
tend vers ![]() avec
avec ![]() . Le
test
est donc nécessairement
unilatéral
à droite (rejet des valeurs trop grandes).
Supposons que la distance
. Le
test
est donc nécessairement
unilatéral
à droite (rejet des valeurs trop grandes).
Supposons que la distance
![]() ait pris la valeur
0.047 pour un
échantillon
de taille
ait pris la valeur
0.047 pour un
échantillon
de taille ![]() 1000. La
statistique
1000. La
statistique
![]() vaut
vaut ![]() 1.486. La
p-valeur
correspondante est :
1.486. La
p-valeur
correspondante est :
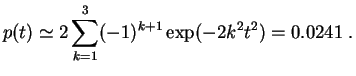
Le test de Kolmogorov-Smirnov s'étend à la comparaison de deux fonctions de répartition empiriques, et permet alors de tester l'hypothèse que deux échantillons sont issus de la même loi. Bien d'autres tests d'ajustement peuvent être utilisés, comme ceux de Stephens, Anderson-Darling et Cramer-von Mises.