Ici, comme dans tout le chapitre, le
modèle
de base est celui d'un
échantillon
d'une loi inconnue ![]() . Les
. Les ![]() données
sont donc
supposées être des réalisations de
variables aléatoires indépendantes,
de même loi
données
sont donc
supposées être des réalisations de
variables aléatoires indépendantes,
de même loi ![]() . Cette loi n'est pas supposée
appartenir à une famille paramétrique particulière (d'où le nom
de
test
non paramétrique). Dans un premier temps,
l'hypothèse
. Cette loi n'est pas supposée
appartenir à une famille paramétrique particulière (d'où le nom
de
test
non paramétrique). Dans un premier temps,
l'hypothèse
![]() portera sur la valeur d'un
quantile
de
portera sur la valeur d'un
quantile
de ![]() .
.
Prenons le cas d'un traitement censé faire baisser le taux de cholestérol.
Pour chaque
individu
![]() d'un groupe de patients, la différence
d'un groupe de patients, la différence ![]() entre
le taux après et avant traitement est mesurée. Certaines de ces
différences sont négatives (diminutions), d'autres positives
(augmentations).
L'hypothèse
entre
le taux après et avant traitement est mesurée. Certaines de ces
différences sont négatives (diminutions), d'autres positives
(augmentations).
L'hypothèse
![]() est que le traitement n'a pas
d'effet significatif. On rejettera
est que le traitement n'a pas
d'effet significatif. On rejettera
![]() (on décidera que le
traitement est efficace) si suffisamment de baisses ont été observées.
La
statistique de test
est le nombre de baisses :
(on décidera que le
traitement est efficace) si suffisamment de baisses ont été observées.
La
statistique de test
est le nombre de baisses :
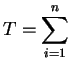 1
1
(La notation
1![]() désigne la fonction indicatrice de l'ensemble
désigne la fonction indicatrice de l'ensemble ![]() ,
qui vaut 1 si
,
qui vaut 1 si ![]() et 0 sinon.)
Si
et 0 sinon.)
Si
![]() est vraie, la
médiane
de la loi
est vraie, la
médiane
de la loi ![]() des
des ![]() est nulle
et
est nulle
et ![]() suit la
loi binomiale
suit la
loi binomiale
![]() .
.
Nous généralisons la situation à la valeur d'un quantile quelconque.
où ![]() est un réel fixé. Soit
est un réel fixé. Soit ![]() le nombre d'éléments de
l'échantillon
inférieurs à
le nombre d'éléments de
l'échantillon
inférieurs à ![]() :
:
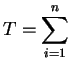 1
1
Sous
l'hypothèse
![]() ,
, ![]() suit la
loi binomiale
suit la
loi binomiale
![]() .
.
Pour un
échantillon
de grande taille, on peut remplacer la
loi binomiale
par son approximation normale. Sous
![]() , la statistique
centrée réduite
:
, la statistique
centrée réduite
:
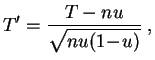
suit approximativement la
loi normale
![]() . Dans l'exemple ci-dessus,
. Dans l'exemple ci-dessus, ![]() prend
la valeur 1.7693.
La
p-valeur
correspondante est :
prend
la valeur 1.7693.
La
p-valeur
correspondante est :