Section : Statistiques de test
Précédent : Règles de décision
Suivant : Tests non paramétriques

Seuil et p-valeur

La définition 1.4 du paragraphe précédent fait apparaître le seuil comme la probabilité $\alpha$, fixée a priori, que le test rejette l'hypothèse ${\cal H}_0$ à tort.

$$\mathbb{P}_{{\cal H}_0}[$$ Rejet de $${\cal H}_0] = \alpha\;.$$

Une fois les données recueillies, la valeur prise par la statistique de test sera calculée, et la réponse sera binaire : rejet ou non de ${\cal H}_0$. On préfère souvent garder l'information contenue dans la valeur de la statistique de test, en retournant le seuil limite auquel ${\cal H}_0$ aurait été rejetée, compte tenu de l'observation.

Prenons l'exemple (fréquent) d'une hypothèse ${\cal H}_0$ sous laquelle la statistique de test $T$ suit la loi normale ${\cal N}(0,1)$. La règle de rejet pour le test bilatéral de seuil 0.05 est :

   Rejet de $${\cal H}_0\;\Longleftrightarrow\; T\notin[-\!1.96\,,\,+\!1.96]\;.$$

Supposons que la valeur prise par $T$ soit 2.72. L'hypothèse ${\cal H}_0$ sera donc rejetée. Mais elle serait également rejetée au seuil 0.01. En fait elle serait rejetée pour n'importe quel seuil supérieur à 0.00653, ce qui est un renseignement plus précis qu'une simple réponse binaire.

Définition 1.7   Soit ${\cal H}_0$ l'hypothèse nulle, $T$ la statistique de test et $F_0$ sa fonction de répartition sous l'hypothèse ${\cal H}_0$. On suppose que $F_0$ est continue.

1. Pour un test bilatéral (rejet des valeurs trop écartées) la p-valeur d'une valeur $t$ prise par $T$ est :
   $$p(t) = \left\{ \begin{array}{lcl} 2F_0(t) &\mbox{si}&F_0(t)... ...(1-F_0(t)) &\mbox{si}&F_0(t)\geq 0.5\;.\\ \end{array}\right.$$

2. Pour un test unilatéral à droite (rejet des valeurs trop grandes) la p-valeur d'une valeur $t$ prise par $T$ est :
   $$p(t) = 1-F_0(t)\;.$$

3. Pour un test unilatéral à gauche (rejet des valeurs trop petites) la p-valeur d'une valeur $t$ prise par $T$ est :
   $$p(t) = F_0(t)\;.$$

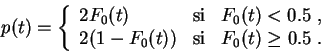
Cependant calculer une p-valeur pour un test bilatéral est assez artificiel. Au vu de la valeur prise par $T$, on aura tendance à effectuer plutôt un test unilatéral visant à décider si la valeur observée est trop grande ou trop petite. Pour une statistique de test suivant la loi ${\cal N}(0,1)$, la valeur 2.72 est clairement à droite de la distribution. Le problème ne se pose plus de savoir si elle est trop petite, mais plutôt si elle est significativement trop grande. En pratique, pour une statistique de test de fonction de répartition $F_0$ sous ${\cal H}_0$, on définira souvent la p-valeur de la valeur $t$ par :

$$p(t) = \min \{F_0(t)\,,\,1\!-\!F_0(t)\}\;.$$

La connaissance de la p-valeur rend inutile le calcul préalable de la région de rejet : si $p(t)$ est la p-valeur d'une observation $t$ sous l'hypothèse ${\cal H}_0$, on obtient un test de seuil $\alpha$ par la règle de rejet :

   Rejet de $${\cal H}_0\;\Longleftrightarrow\; p(T)<\alpha\;.$$

Dans le cas continu, ceci revient à remplacer la statistique $T$ par $F_0(T)$ ou $1-F_0(T)$. Sous l'hypothèse ${\cal H}_0$, ces deux statistiques suivent la loi uniforme ${\cal U}(0,1)$.

Quand la statistique de test est discrète, il faut inclure la valeur observée dans l'intervalle dont on calcule la probabilité. Pour un test unilatéral à gauche, cela n'induit pas de changement : $F_0(t)$ est la probabilité que $T$ soit inférieure ou égale à $t$. Pour un test unilatéral à droite sur une variable à valeurs dans $\mathbb{N}$ (le cas le plus fréquent) il faudra calculer $1-F_0(t\!-\!1)$. Supposons par exemple que la loi de $T$ soit la loi binomiale ${\cal B}(100,0.5)$, la p-valeur de 60 est la probabilité que $T$ soit supérieure ou égale à 60, à savoir :

$$1-F_{{\cal B}(100,0.5)}(59) = 0.0284\;.$$

Section : Statistiques de test
Précédent : Règles de décision
Suivant : Tests non paramétriques