Un
modèle probabiliste
a donc été choisi, qui fait des données
observées des réalisations de
variables aléatoires.
Notons
![]() les
données
et
les
données
et
![]() les
variables aléatoires
qui les modélisent. Sur la loi
de ces
variables aléatoires,
un certain nombre
d'hypothèses
sont
émises et ne seront pas remises en cause. Une
hypothèse
particulière,
les
variables aléatoires
qui les modélisent. Sur la loi
de ces
variables aléatoires,
un certain nombre
d'hypothèses
sont
émises et ne seront pas remises en cause. Une
hypothèse
particulière,
![]() doit être testée. La décision va
porter sur la valeur prise par une certaine fonction
doit être testée. La décision va
porter sur la valeur prise par une certaine fonction ![]() des
données
:
des
données
:
Pour la
loi de probabilité
![]() , les valeurs
les plus plausibles sont contenues dans ses
intervalles de dispersion
. Ils s'expriment à l'aide de la
fonction quantile.
Si
, les valeurs
les plus plausibles sont contenues dans ses
intervalles de dispersion
. Ils s'expriment à l'aide de la
fonction quantile.
Si ![]() est une
variable aléatoire,
la
fonction quantile
de la loi de
est une
variable aléatoire,
la
fonction quantile
de la loi de ![]() est la fonction de [0,1] dans
est la fonction de [0,1] dans
![]() qui à
qui à
![]() [0,1] associe :
[0,1] associe :
C'est l'inverse de la fonction de répartition. Les fonctions quantile, comme les fonctions de répartition. de toutes les lois usuelles sont disponibles dans les environnements de calcul courants.
Un
intervalle de dispersion
de niveau
![]() pour
pour ![]() est tel que
est tel que ![]() appartient à cet intervalle avec
probabilité
appartient à cet intervalle avec
probabilité
![]() . Il contient donc une forte proportion
des valeurs que prendra
. Il contient donc une forte proportion
des valeurs que prendra ![]() , même s'il est en général beaucoup plus petit
que le support de la loi.
, même s'il est en général beaucoup plus petit
que le support de la loi.
Selon les valeurs de ![]() , on dit qu'un
intervalle de dispersion
de niveau
, on dit qu'un
intervalle de dispersion
de niveau
![]() est :
est :
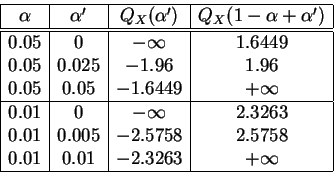
Fixons
![]() 0.9. En toute rigueur, la valeur de la
fonction quantile,
au point 0.9 est 7. L'intervalle [0,7] devrait donc être un
intervalle de dispersion
de niveau 0.9 pour la loi
0.9. En toute rigueur, la valeur de la
fonction quantile,
au point 0.9 est 7. L'intervalle [0,7] devrait donc être un
intervalle de dispersion
de niveau 0.9 pour la loi
![]() . Pourtant
sa
probabilité
n'est que de 0.833. Pour les calculs utilisant
les
intervalles de dispersion,
on applique toujours un principe de
précaution, qui consiste à garantir le niveau. On ne qualifiera donc
d'intervalle de dispersion
de niveau
. Pourtant
sa
probabilité
n'est que de 0.833. Pour les calculs utilisant
les
intervalles de dispersion,
on applique toujours un principe de
précaution, qui consiste à garantir le niveau. On ne qualifiera donc
d'intervalle de dispersion
de niveau
![]() que les intervalles
dont la
probabilité
est supérieure ou égale à
que les intervalles
dont la
probabilité
est supérieure ou égale à
![]() .
Ce principe amène à modifier la définition 1.3 pour
les
lois discrètes
à valeurs dans
.
Ce principe amène à modifier la définition 1.3 pour
les
lois discrètes
à valeurs dans
![]() , en remplaçant la borne de
droite
, en remplaçant la borne de
droite
![]() par
par
![]() .
Le tableau ci-dessous donne la liste des intervalles de dispersion
de niveau
.
Le tableau ci-dessous donne la liste des intervalles de dispersion
de niveau ![]() 0.9, avec leur
probabilité
exacte,
pour la loi
0.9, avec leur
probabilité
exacte,
pour la loi
![]() .
.
Deux intervalles sont d'amplitude minimale, [3,8] et [4,9]. On choisira celui dont la probabilité est la plus proche du niveau prescrit, à savoir [4,9].
Un
test
consistera à rejeter
l'hypothèse
![]() si la valeur prise par la
statistique de test
est en dehors d'un
intervalle de dispersion
de niveau donné.
si la valeur prise par la
statistique de test
est en dehors d'un
intervalle de dispersion
de niveau donné.
Le complémentaire de ![]() s'appelle la région de rejet.
Si
s'appelle la région de rejet.
Si
![]() est vraie, le
seuil
est vraie, le
seuil
![]() est la probabilité
que la valeur prise par
est la probabilité
que la valeur prise par ![]() soit en dehors de
soit en dehors de ![]() , et donc que
, et donc que
![]() soit rejetée à tort.
soit rejetée à tort.
Nous avons laissé jusqu'ici une grande latitude quant au choix de l'intervalle de dispersion. Les intervalles les plus utilisés sont symétriques ou unilatéraux.
Dans le cas de l'efficacité d'un médicament, avec le nombre de guérisons comme statistique de test, on choisira un test unilatéral (le traitement est inefficace si la fréquence de guérison est trop faible, efficace si elle est suffisamment grande). Pour tester un générateur pseudo-aléaoire, avec le nombre d'appels entre 0.4 et 0.9 comme statistique de test, on rejettera aussi bien les valeurs trop grandes que trop petites, et le sera bilatéral.
Nous résumons dans la définition suivante les trois types de tests usuels.
Supposons que la
statistique de test
![]() suive sous
suive sous
![]() la loi
binomiale
la loi
binomiale
![]() , comme dans l'exemple du
générateur pseudo-aléatoire.
L'intervalle de dispersion
symétrique de niveau
, comme dans l'exemple du
générateur pseudo-aléatoire.
L'intervalle de dispersion
symétrique de niveau
![]() 0.05 est [40,60]. Le
test bilatéral
de
seuil
0.05
consistera à rejeter
0.05 est [40,60]. Le
test bilatéral
de
seuil
0.05
consistera à rejeter
![]() si la
statistique de test
prend une
valeur inférieure à 40 ou supérieure à 60. Pour la loi
binomiale,
comme pour d'autres, on peut choisir d'utiliser l'approximation
normale : si
si la
statistique de test
prend une
valeur inférieure à 40 ou supérieure à 60. Pour la loi
binomiale,
comme pour d'autres, on peut choisir d'utiliser l'approximation
normale : si ![]() est assez grand, la loi
est assez grand, la loi
![]() est proche de
la
loi normale
de même
espérance
et de même
variance.
Ici, la loi de
est proche de
la
loi normale
de même
espérance
et de même
variance.
Ici, la loi de
![]() est proche de la loi
est proche de la loi
![]() .
L'intervalle de dispersion
symétrique de niveau 0.95 pour cette loi est
[40.2,59.8].
D'après cet intervalle, on devrait aussi rejeter
les valeurs 40 et 60. Ce genre d'approximation était d'usage
courant quand on ne disposait que de tables de
quantiles.
Les environnements
de calcul sont désormais capables d'effectuer des calculs précis
de n'importe quel
quantile
pour toutes les lois usuelles. En règle
générale, il faut éviter d'utiliser un résultat
d'approximation quand un calcul exact est possible.
.
L'intervalle de dispersion
symétrique de niveau 0.95 pour cette loi est
[40.2,59.8].
D'après cet intervalle, on devrait aussi rejeter
les valeurs 40 et 60. Ce genre d'approximation était d'usage
courant quand on ne disposait que de tables de
quantiles.
Les environnements
de calcul sont désormais capables d'effectuer des calculs précis
de n'importe quel
quantile
pour toutes les lois usuelles. En règle
générale, il faut éviter d'utiliser un résultat
d'approximation quand un calcul exact est possible.
Les
quantiles
de la loi
![]() n'ont jamais été tabulés.
Pour les calculer, on se ramenait à la loi
n'ont jamais été tabulés.
Pour les calculer, on se ramenait à la loi
![]() , en
remplaçant la
statistique de test
, en
remplaçant la
statistique de test
![]() par sa valeur
centrée réduite.
par sa valeur
centrée réduite.
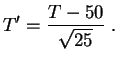
Si on admet que la variable ![]() suit la loi
suit la loi
![]() , le test
bilatéral
de
seuil
0.05 consiste à rejeter toute valeur à l'extérieur
de
l'intervalle de dispersion
[-1.96,+1.96]. C'est évidemment
équivalent au fait de rejeter les valeurs de
, le test
bilatéral
de
seuil
0.05 consiste à rejeter toute valeur à l'extérieur
de
l'intervalle de dispersion
[-1.96,+1.96]. C'est évidemment
équivalent au fait de rejeter les valeurs de ![]() à l'extérieur
de l'intervalle [40.2,59.8]. D'autres transformations sont possibles.
Si
à l'extérieur
de l'intervalle [40.2,59.8]. D'autres transformations sont possibles.
Si ![]() suit la loi
suit la loi
![]() , alors
, alors
![]() suit la
loi du chi-deux
suit la
loi du chi-deux
![]() . Rejeter les valeurs de
. Rejeter les valeurs de ![]() à l'extérieur
de l'intervalle [-1.96,+1.96] est équivalent à rejeter les
valeurs de
à l'extérieur
de l'intervalle [-1.96,+1.96] est équivalent à rejeter les
valeurs de ![]() supérieures à
supérieures à
![]() , qui est effectivement
le
quantile
d'ordre 0.95 de la loi
, qui est effectivement
le
quantile
d'ordre 0.95 de la loi
![]() . Remarquons qu'un
test
bilatéral
sur la
statistique
. Remarquons qu'un
test
bilatéral
sur la
statistique
![]() est équivalent à un
test
unilatéral
à droite sur la
statistique
est équivalent à un
test
unilatéral
à droite sur la
statistique
![]() .
.
Les chapitres 2 et 3
contiennent les exemples les plus classiques de
tests,
d'abord
sur les
quantiles,
ensuite dans le cadre
gaussien.
Nous ne préciserons
pas toujours s'il s'agit de
tests
bilatéraux
ou
unilatéraux.
L'important est de décrire
l'hypothèse
![]() , la
statistique de test
, la
statistique de test
![]() et sa loi sous
et sa loi sous
![]() . Décider si le
test doit être
unilatéral
à gauche ou à droite ou bien
bilatéral
est le plus
souvent affaire de bon sens.
. Décider si le
test doit être
unilatéral
à gauche ou à droite ou bien
bilatéral
est le plus
souvent affaire de bon sens.