Section : Estimation ponctuelle
Précédent : Intervalles de dispersion
Suivant : Recherche d'estimateurs

Exemples d'estimateurs

Dans cette section, nous illustrons les notions d'estimateur, de convergence et de biais sur trois exemples, l'estimation d'une variance, le problème des questions confidentielles, et les comptages par capture-recapture.

Estimateurs de la variance.

Soit $(X_1,\ldots,X_n)$ un échantillon d'une loi inconnue $P$, qui sera supposée admettre des moments de tous ordres. Nous avons vu que la moyenne empirique $\overline{X}_n=(X_1+\cdots+X_n)/n$ est un estimateur convergent de l'espérance. C'est un estimateur sans biais, et sa variance est égale à la variance de la loi $P$, divisée par $n$. Comment estimer la variance de $P$ ? L'estimateur le plus naturel est le suivant.

Définition 1.11   On appelle variance empirique de l'échantillon $(X_1,\ldots,X_n)$ l'estimateur :

$$S^2_n = \frac{X_1^1+\cdots+X_n^2}{n} - \overline{X}_n^2\;.$$

Si $X$ désigne une variable aléatoire de loi $P$, $(X_1^2+\cdots+X_n^2)/n$ est un estimateur convergent de $\mathbb{E}[X^2]$. Comme $\overline{X}_n^2$ est un estimateur convergent de $(\mathbb{E}[X])^2$, $S^2_n$ est bien un estimateur convergent de $Var[X]=\mathbb{E}[X^2]-(\mathbb{E}[X])^2$. Mais ce n'est pas un estimateur sans biais. En effet :

Proposition 1.12  

$$\mathbb{E}[S^2_n] = \frac{n-1}{n}Var[X]\;.$$

Démonstration : Calculons tout d'abord $\mathbb{E}[\overline{X}^2_n]$.

$$\begin{array}{ccc} \mathbb{E}[\overline{X}_n^2]&=&\frac{1}{n... ...X_i^2 + \sum_{i=1}^n\sum_{j\neq i} X_iX_j\right]\;. \end{array}$$

Par définition d'un échantillon, $X_1,\ldots,X_n$ sont indépendantes et de même loi. Donc $\mathbb{E}[X_i^2]=\mathbb{E}[X^2]$ et $\mathbb{E}[X_iX_j]=(\mathbb{E}[X])^2$. En reportant ces valeurs on obtient :

$$\begin{array}{ccc} \mathbb{E}[\overline{X}^2_n]&=&\frac{1}{n... ...mathbb{E}[X^2] + \frac{n-1}{n} (\mathbb{E}[X])^2\;. \end{array}$$

On a donc :

$$\begin{array}{ccc} \mathbb{E}[S^2_n]&=&\frac{1}{n}\mathbb{E}[... ...} (\mathbb{E}[X])^2)\\ &=&\frac{n-1}{n}Var[X]\;. \end{array}$$

$\square$

Pour transformer $S^2_n$ en un estimateur non biaisé, il suffit de corriger le biais par un facteur multiplicatif.

Définition 1.13   On appelle variance empirique non biaisée l'estimateur :

$$V_n = \frac{n}{n-1} S^2_n\;.$$

On peut estimer l'écart-type par $\sqrt{S^2_n}$ ou bien $\sqrt{V_n}$. Notons qu'en général aussi bien $\sqrt{V_n}$ que $\sqrt{S^2_n}$ sont des estimateurs biaisés de $\sqrt{Var[X]}$. La différence entre les deux estimateurs tend vers 0 quand la taille $n$ de l'échantillon tend vers l'infini. Néanmoins, la plupart des calculatrices proposent les deux estimateurs de l'écart-type (touches $\sigma_n$ et $\sigma_{n-1}$). Certains logiciels (en particulier Scilab) calculent par défaut la valeur de $V_n$ ou $\sqrt{V_n}$, d'autres $S^2_n$ ou $\sqrt{S^2_n}$. Dans la suite, nous utiliserons surtout $S^2_n$, malgré l'inconvénient du biais.

Questions confidentielles.

Certains sujets abordés dans les enquêtes d'opinion sont parfois assez intimes, et on court le risque que les personnes interrogées se refusent à répondre franchement à l'enquêteur, faussant ainsi le résultat. On peut alors avoir recours à une astuce consistant à inverser aléatoirement les réponses . Considérons une question confidentielle pour laquelle on veut estimer la probabilité $p$ de réponses positives. L'enquêteur demande à chaque personne interrogée de lancer un dé. Si le dé tombe sur $6$, la personne doit donner sa réponse sans mentir, sinon elle doit donner l'opinion contraire à la sienne. Si l'enquêteur ignore le résultat du dé, il ne pourra pas savoir si la réponse est franche ou non, et on peut espérer que la personne sondée acceptera de jouer le jeu. Généralisons légèrement la situation en tirant pour chaque personne une variable de Bernoulli de paramètre $\alpha$. Si le résultat de cette variable est 1, la réponse est franche, sinon, elle est inversée. Soit $n$ le nombre de personnes interrogées. L'enquêteur ne recueille que la fréquence empirique $F_n$ des ``oui''. La proportion inconnue des ``oui'' à l'issue de la procédure est $q=\alpha p + (1-\alpha)(1-p)$, et la fréquence $F_n$ observée par l'enquêteur est un estimateur sans biais et convergent de $q$. Remarquons que si $\alpha=1/2$, $q$ vaut 1/2 quel que soit $p$. Mais si $\alpha\neq$ 1/2, on peut exprimer $p$ en fonction de $q$ :

$$p=\frac{q-1+\alpha}{2\alpha-1}\;.$$

On peut donc proposer comme estimateur de $p$ la quantité suivante :

$$T_n=\frac{F_n-1+\alpha}{2\alpha-1}\;.$$

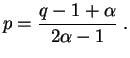
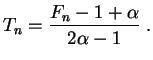
L'espérance de $T_n$ est $p$. La variance de $T_n$ vaut :

$$\frac{q(1-q)}{n(2\alpha-1)^2} = \frac{p(1-p)}{n} + \frac{\alpha(1-\alpha)}{n(2\alpha-1)^2}\;.$$

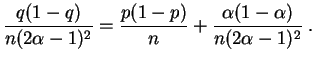
L'estimateur $T_n$ est sans biais, sa variance tend vers 0, il est donc convergent.

Pour $n$ fixé, la variance de $T$ tend vers l'infini quand $\alpha$ tend vers 1/2. Elle est minimale si $\alpha=$0 ou 1 (mais alors la procédure perd tout son intérêt). Le problème est donc de choisir une valeur de $\alpha$ qui soit assez grande pour que la confidentialité soit crédible, mais suffisamment éloignée de 1/2 pour ne pas trop augmenter la variance de l'estimateur. Pour le dé, la valeur de $\alpha$ est 1/6 et le terme additionnel de la variance est proportionnel à $\alpha(1-\alpha)/(2\alpha-1)^2 =$0.3125.

Comptages par capture-recapture

Comment estimer le nombre d'espèces d'insectes vivant sur la terre, alors que de nombreuses espèces sont encore inconnues ? Comment connaît-on la population de baleines dans les océans ? Le comptage par capture-recapture permet d'évaluer des tailles de population pour lesquelles un recensement exhaustif est impossible. La méthode est basée sur une idée simple. Considérons une population, de taille $N$ inconnue. On prélève dans un premier temps un groupe d'individus, de taille $m$ fixée. Ces individus sont recensés et marqués de façon à être reconnus ultérieurement. Plus tard, on prélève un nouveau groupe de taille $n$, et on observe le nombre $X$ d'individus marqués dans ce nouveau groupe. Si le deuxième prélèvement est indépendant du premier, la loi de $X$ est la loi hypergéométrique de paramètres $N$, $m$ et $n$, d'espérance $nm/N$. On peut s'attendre à ce que la proportion $X/n$ d'individus marqués dans le deuxième échantillon soit proche de la proportion d'individus marqués dans l'ensemble de la population, $m/N$. Il est donc raisonnable de proposer comme estimateur de $N$ la quantité suivante :

$$T=\frac{nm}{X}\;.$$

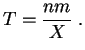
L'inconvénient de cet estimateur est qu'il n'est pas défini si $X$ prend la valeur 0, ce qui arrive avec une probabilité strictement positive. On peut corriger ce défaut de deux manières. La première consiste à remplacer $X$ par $X+1$, ce qui ne devrait pas fausser trop le résultat si les nombres envisagés sont assez grands. Posons donc :

$$T'=\frac{nm}{X+1}\;.$$

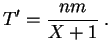
La seconde manière consiste à décider de rejeter a priori les échantillons pour lesquels on n'obtiendrait pas d'individu marqué. Ceci revient à remplacer $X$ par une autre variable aléatoire $X'$ dont la loi est la loi conditionnelle de $X$ sachant que $X$ est strictement positif. Posons donc

$$T'' = \frac{nm}{X'}\;.$$

Pour des valeurs de $N$, $m$ et $n$ particulières, on peut calculer numériquement les espérances et les écart-types de ces estimateurs. Le tableau ci-dessous résume des résultats obtenus pour $m=n=$100 et différentes valeurs de $N$.

$N$	200	300	400	500	1000	5000
$\mathbb{E}[T']$	197.0	295.1	393.1	491.1	981.3	4291.1
$\sqrt{Var[T']}$	13.9	34.4	60.2	90.7	309.3	2459.5
$\mathbb{E}[T'']$	201.0	304.2	409.6	517.5	1102.0	5767.9
$\sqrt{Var[T'']}$	14.5	36.6	65.6	101.5	420.2	2995.4

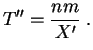
Les deux estimateurs sont biaisés, le premier a tendance à sous-estimer $N$, le deuxième à le sur-estimer. L'écart-type augmente plus rapidement que $N$. Il est naturel que la précision relative soit d'autant plus faible que les échantillons recueillis sont petits devant la taille inconnue de la population.

Section : Estimation ponctuelle
Précédent : Intervalles de dispersion
Suivant : Recherche d'estimateurs