Section : Estimation ponctuelle
Précédent : Qualités d'un estimateur
Suivant : Exemples d'estimateurs
L'erreur quadratique
mesure la concentration d'un
estimateur
autour
de la valeur du paramètre. Les
intervalles de dispersion
sont un
autre moyen de mesurer la plus ou moins grande concentration d'une
loi de probabilité.
Ils s'expriment à l'aide de la
fonction quantile.
Si 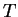 est une
variable aléatoire,
la
fonction quantile
de la loi de
est une
variable aléatoire,
la
fonction quantile
de la loi de
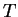 est la fonction de [0,1] dans
est la fonction de [0,1] dans
 qui à
qui à 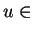 [0,1] associe :
[0,1] associe :
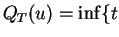
t.q.
![$\displaystyle \mathbb{P}[T\leq t]\geq u\}\;.
$](img63.gif)
En statistique, les réels 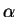 compris entre 0 et
1 sont de tradition. La même tradition leur affecte prioritairement les
valeurs 0.05 et 0.01, plus rarement 0.02, 0.005 ou 0.001. Il
faut donc lire
compris entre 0 et
1 sont de tradition. La même tradition leur affecte prioritairement les
valeurs 0.05 et 0.01, plus rarement 0.02, 0.005 ou 0.001. Il
faut donc lire 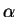 comme ''une faible proportion'', et
comme ''une faible proportion'', et
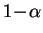 comme ''une forte proportion''. Un
intervalle de dispersion
de niveau
comme ''une forte proportion''. Un
intervalle de dispersion
de niveau
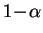 pour
pour 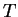 est tel que
est tel que 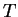 appartient à cet intervalle avec
probabilité
appartient à cet intervalle avec
probabilité
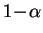 . Il contient donc une forte proportion
des valeurs que prendra
. Il contient donc une forte proportion
des valeurs que prendra 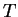 , même s'il est en général beaucoup plus petit
que le support de la loi.
, même s'il est en général beaucoup plus petit
que le support de la loi.
Selon les valeurs de 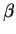 , on dit qu'un intervalle de dispersion
de niveau
, on dit qu'un intervalle de dispersion
de niveau
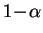 est :
est :
-
unilatéral
inférieur si
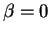 ,
,
-
unilatéral
supérieur si
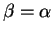 ,
,
- symétrique si
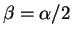 ,
,
- optimal si son amplitude est la plus courte parmi tous
les
intervalles de dispersion
de niveau
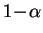 .
.
Déterminer un
intervalle de dispersion
optimal requiert en général
un calcul numérique particulier, sauf dans le cas où la loi est
symétrique, comme une
loi normale
ou une
loi de Student.
On dit que la loi
de 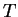 est symétrique si pour tout
est symétrique si pour tout 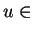 [0,1],
[0,1],
On démontre que si la loi de 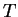 est symétrique, alors l'intervalle
de dispersion symétrique est optimal.
est symétrique, alors l'intervalle
de dispersion symétrique est optimal.
La notion de convergence se traduit en termes
d'intervalles de dispersion
de la façon suivante.
Démonstration : Dire qu'un
estimateur
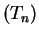 est convergent, c'est dire que la probabilité
que
est convergent, c'est dire que la probabilité
que 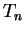 appartienne à l'intervalle
appartienne à l'intervalle
![$ [\theta-\varepsilon , \theta+\varepsilon]$](img77.gif) tend vers 1 quand la taille
tend vers 1 quand la taille 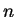 de
l'échantillon
tend vers l'infini. Si
de
l'échantillon
tend vers l'infini. Si 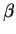 est différent de 0, il
existe
est différent de 0, il
existe 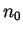 tel que pour
tel que pour 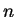 supérieur à
supérieur à 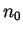 , la
probabilité
que
, la
probabilité
que
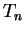 soit inférieur à
soit inférieur à
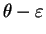 , est inférieure
à
, est inférieure
à 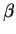 . Ceci équivaut à dire que
. Ceci équivaut à dire que
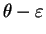 est inférieur
à
est inférieur
à
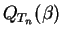 . De même si
. De même si
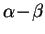 est différent de 0,
il existe
est différent de 0,
il existe 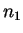 tel que pour
tel que pour 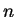 supérieur à
supérieur à 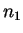 , la
probabilité
que
, la
probabilité
que
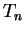 soit inférieur à
soit inférieur à
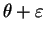 , est supérieure
à
, est supérieure
à
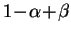 . Ceci équivaut à dire que
. Ceci équivaut à dire que
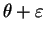 est supérieur à
est supérieur à
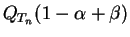 .
Donc pour
.
Donc pour 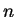 supérieur à
supérieur à 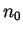 et
et 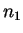 , l'intervalle de
dispersion
, l'intervalle de
dispersion
![$ [\,Q_{T_n}(\beta),Q_{T_n}(1-\alpha+\beta)\,]$](img76.gif) est
inclus dans l'intervalle
est
inclus dans l'intervalle
![$ [\theta-\varepsilon , \theta+\varepsilon]$](img77.gif) .
.
Réciproquement, si
![$ [\,Q_{T_n}(\beta),Q_{T_n}(1-\alpha+\beta)\,]$](img76.gif) est inclus dans
est inclus dans
![$ [\theta-\varepsilon , \theta+\varepsilon]$](img77.gif) à partir d'un certain
à partir d'un certain 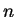 ,
alors la
probabilité
que
,
alors la
probabilité
que 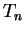 soit compris entre
soit compris entre
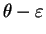 et
et
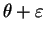 est supérieure à
est supérieure à 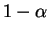 . Ceci étant
vrai pour tout
. Ceci étant
vrai pour tout 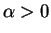 , cette
probabilité
tend vers 1.
, cette
probabilité
tend vers 1.
A titre d'exemple, nous reprenons
l'estimateur
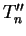 pour la loi
uniforme
pour la loi
uniforme
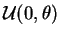 , à savoir le maximum des valeurs de
l'échantillon.
Sa
fonction quantile
est la fonction qui à
, à savoir le maximum des valeurs de
l'échantillon.
Sa
fonction quantile
est la fonction qui à 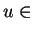 [0,1]
associe :
[0,1]
associe :
Pour 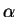 et
et
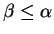 fixés,
l'intervalle de dispersion
fixés,
l'intervalle de dispersion
![$ [\,Q_{T''_n}(\beta),Q_{T''_n}(1-\alpha+\beta)\,]$](img90.gif) a pour longueur :
Il se trouve que
l'intervalle de dispersion
optimal coïncide avec
l'intervalle de dispersion
unilatéral
supérieur (
a pour longueur :
Il se trouve que
l'intervalle de dispersion
optimal coïncide avec
l'intervalle de dispersion
unilatéral
supérieur (
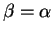 ).
La borne de gauche est
).
La borne de gauche est
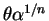 , la borne de droite est
, la borne de droite est
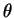 .
Voici quelques valeurs pour la quantité
.
Voici quelques valeurs pour la quantité
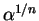 , qui tend vers
1 quand
, qui tend vers
1 quand 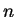 tend vers l'infini.
tend vers l'infini.
Quand la loi de la
variable aléatoire
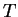 est discrète, la notion
d'intervalle de dispersion
recèle une certaine ambiguïté. Considérons
par exemple la
loi binomiale
est discrète, la notion
d'intervalle de dispersion
recèle une certaine ambiguïté. Considérons
par exemple la
loi binomiale
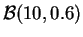 . Voici les valeurs de sa
fonction de répartition.
. Voici les valeurs de sa
fonction de répartition.
Fixons
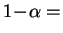 0.9. En toute rigueur, la valeur de la
fonction quantile.
au point 0.9 est 7. L'intervalle [0,7] devrait donc être un
intervalle de dispersion
de niveau 0.9 pour la loi
0.9. En toute rigueur, la valeur de la
fonction quantile.
au point 0.9 est 7. L'intervalle [0,7] devrait donc être un
intervalle de dispersion
de niveau 0.9 pour la loi
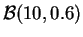 . Pourtant
sa
probabilité
n'est que de 0.833. Pour les calculs utilisant
les
intervalles de dispersion,
on applique toujours un principe de
précaution, qui consiste à garantir le niveau. On ne qualifiera donc
d'intervalle de dispersion
de niveau
. Pourtant
sa
probabilité
n'est que de 0.833. Pour les calculs utilisant
les
intervalles de dispersion,
on applique toujours un principe de
précaution, qui consiste à garantir le niveau. On ne qualifiera donc
d'intervalle de dispersion
de niveau
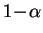 que les intervalles
dont la
probabilité
est supérieure ou égale à
que les intervalles
dont la
probabilité
est supérieure ou égale à
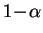 .
Ce principe amène à modifier la définition 1.9 pour
les
lois discrètes
à valeurs dans
.
Ce principe amène à modifier la définition 1.9 pour
les
lois discrètes
à valeurs dans
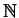 , en remplaçant la borne de
droite
, en remplaçant la borne de
droite
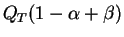 par
par
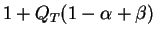 .
Le tableau ci-dessous donne la liste des intervalles de dispersion
de niveau
.
Le tableau ci-dessous donne la liste des intervalles de dispersion
de niveau 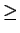 0.9, avec leur
probabilité
exacte,
pour la loi
0.9, avec leur
probabilité
exacte,
pour la loi
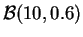 .
.
Deux intervalles sont d'amplitude minimale, [3,8] et [4,9].
On choisira celui dont la
probabilité
est la plus proche du
niveau prescrit,à savoir [4,9].
Section : Estimation ponctuelle
Précédent : Qualités d'un estimateur
Suivant : Exemples d'estimateurs
![]() est une
variable aléatoire,
la
fonction quantile
de la loi de
est une
variable aléatoire,
la
fonction quantile
de la loi de
![]() est la fonction de [0,1] dans
est la fonction de [0,1] dans
![]() qui à
qui à ![]() [0,1] associe :
[0,1] associe :
![]() compris entre 0 et
1 sont de tradition. La même tradition leur affecte prioritairement les
valeurs 0.05 et 0.01, plus rarement 0.02, 0.005 ou 0.001. Il
faut donc lire
compris entre 0 et
1 sont de tradition. La même tradition leur affecte prioritairement les
valeurs 0.05 et 0.01, plus rarement 0.02, 0.005 ou 0.001. Il
faut donc lire ![]() comme ''une faible proportion'', et
comme ''une faible proportion'', et
![]() comme ''une forte proportion''. Un
intervalle de dispersion
de niveau
comme ''une forte proportion''. Un
intervalle de dispersion
de niveau
![]() pour
pour ![]() est tel que
est tel que ![]() appartient à cet intervalle avec
probabilité
appartient à cet intervalle avec
probabilité
![]() . Il contient donc une forte proportion
des valeurs que prendra
. Il contient donc une forte proportion
des valeurs que prendra ![]() , même s'il est en général beaucoup plus petit
que le support de la loi.
, même s'il est en général beaucoup plus petit
que le support de la loi.
![]() , on dit qu'un intervalle de dispersion
de niveau
, on dit qu'un intervalle de dispersion
de niveau
![]() est :
est :
![]() est symétrique, alors l'intervalle
de dispersion symétrique est optimal.
est symétrique, alors l'intervalle
de dispersion symétrique est optimal.
![]() est inclus dans
est inclus dans
![]() à partir d'un certain
à partir d'un certain ![]() ,
alors la
probabilité
que
,
alors la
probabilité
que ![]() soit compris entre
soit compris entre
![]() et
et
![]() est supérieure à
est supérieure à ![]() . Ceci étant
vrai pour tout
. Ceci étant
vrai pour tout ![]() , cette
probabilité
tend vers 1.
, cette
probabilité
tend vers 1.![]()
![]() pour la loi
uniforme
pour la loi
uniforme
![]() , à savoir le maximum des valeurs de
l'échantillon.
Sa
fonction quantile
est la fonction qui à
, à savoir le maximum des valeurs de
l'échantillon.
Sa
fonction quantile
est la fonction qui à ![]() [0,1]
associe :
[0,1]
associe :
![]() est discrète, la notion
d'intervalle de dispersion
recèle une certaine ambiguïté. Considérons
par exemple la
loi binomiale
est discrète, la notion
d'intervalle de dispersion
recèle une certaine ambiguïté. Considérons
par exemple la
loi binomiale
![]() . Voici les valeurs de sa
fonction de répartition.
. Voici les valeurs de sa
fonction de répartition.