Section : Estimation ponctuelle
Précédent : Estimateurs et estimations
Suivant : Intervalles de dispersion

Qualités d'un estimateur

Pour un échantillon de taille $n$ de la loi de Bernoulli de paramètre inconnu $p$, la variable aléatoire égale à la somme des composantes divisée par $n$ (la fréquence empirique), est un estimateur de $p$. C'est une variable aléatoire qui prend ses valeurs dans [0,1]. Si $n$ est grand, elle prend avec une forte probabilité des valeurs proches de $p$, d'après la loi des grands nombres. Quel que soit le modèle et le paramètre à estimer, prendre des valeurs proches de ce paramètre au moins pour de grands échantillons, est la qualité principale que l'on attend d'un estimateur. En toute rigueur, on doit considérer une suite d'estimateurs $(T_n)$, où pour tout $n$, $T_n$ est une variable aléatoire fonction de l'échantillon $(X_1,\ldots,X_n)$. Par abus de langage, on appelle encore ``estimateur'' cette suite.

Définition 1.2   On dit que l'estimateur $(T_n)$ est convergent si pour tout $\varepsilon >0$,

$$\lim_{n\rightarrow\infty}P[ \vert T_n-\theta\vert>\varepsilon ] = 0\;.$$

Un estimateur convergent s'écarte donc du paramètre avec une faible probabilité, si la taille de l'échantillon est assez grande.

L'exemple de base d'estimateur convergent est la moyenne empirique. Nous noterons $\overline{X}_n$ la moyenne empirique de l'échantillon $(X_1,\ldots,X_n)$ :

$$\overline{X}_n = \frac{X_1+\cdots+X_n}{n}\;.$$

La loi faible des grands nombres affirme que $\overline{X}_n$ est un estimateur convergent de l'espérance de $X$.

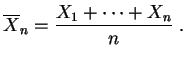
Si le paramètre $\theta$ s'exprime comme une fonction continue de $\mathbb{E}[X]$, alors l'image de $\overline{X}_n$ par cette fonction est un estimateur convergent de $\theta$, par la proposition suivante.

Proposition 1.3   Soit $(T_n)$ un estimateur convergent du paramètre $\theta$, et $\phi$ une fonction de $\mathbb{R}$ dans $\mathbb{R}$, continue au point $\theta$. Alors $(\phi(T_n))$ est un estimateur convergent de $\phi(\theta)$.

Considérons par exemple comme modèle la loi uniforme sur $[0,\theta]$, où le paramètre $\theta$ est inconnu. La moyenne empirique $\overline{X}_n$ est un estimateur convergent de l'espérance de la loi, qui vaut $\theta/2$. Donc $T_n=2\overline{X}_n$ est un estimateur convergent de $\theta$.

Mais d'autres espérances sont calculables. Par exemple, si $X$ suit la loi uniforme sur $[0,\theta]$, alors $\mathbb{E}[\log(X)]$ vaut $\log(\theta)-1$. Toujours d'après la loi des grands nombres, $(\log(X_1)+\cdots+\log(X_n))/n$ est un estimateur convergent de $\log(\theta)-1$. Donc l'estimateur $T'_n$ suivant est encore un estimateur convergent de $\theta$ :

$$T'_n = \exp\Big(\frac{\log(X_1)+\cdots+\log(X_n)}{n}+1\Big)\;.$$

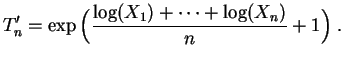
La notion de convergence ne donne aucune assurance pratique que les valeurs prises par un estimateur seront effectivement dans un rayon fixé autour de la vraie valeur du paramètre, pour une taille d'échantillon donnée. On quantifie la qualité des estimateurs par la notion d'erreur quadratique.

Définition 1.4   On appelle erreur quadratique de $T_n$ par rapport à $\theta$ la quantité :

$$EQ(T_n,\theta) = \mathbb{E}[(T_n-\theta)^2]\;.$$

L'erreur quadratique est liée à la convergence par la proposition suivante.

Proposition 1.5   Si l'erreur quadratique de $T_n$ par rapport à $\theta$ tend vers 0 quand $n$ tend vers l'infini, alors $(T_n)$ est un estimateur convergent de $\theta$.

Démonstration : Si $\vert T_n-\theta\vert>\varepsilon$, alors $(T_n-\theta)^2>\varepsilon^2$. Donc :

$$\mathbb{E}[(T_n-\theta)^2] > \varepsilon^2 \mathbb{P}[\vert T_n-\theta\vert>\varepsilon]\;.$$

Si $\mathbb{E}[(T_n-\theta)^2]$ tend vers 0, il en est de même de $\mathbb{P}[\vert T_n-\theta\vert>\varepsilon]$.$\square$Si deux estimateurs sont disponibles pour le même paramètre $\theta$, on dira que l'un est meilleur que l'autre si son erreur quadratique par rapport à $\theta$ est inférieure. Dans l'exemple ci-dessus, l'erreur quadratique de $T_n$ vaut $\theta^2/(3 n)$, l'erreur quadratique de $T'_n$ est équivalente à $\theta^2/n$ quand $n$ tend vers l'infini, $T_n$ est donc meilleur que $T'_n$.

Même pour un estimateur convergent, il peut se faire que les valeurs prises soient décalées en moyenne par rapport à la vraie valeur du paramètre. On dit alors que l'estimateur est biaisé .

Définition 1.6   On appelle biais de l'estimateur $T_n$ par rapport à $\theta$ la quantité :

$$B(T_n,\theta) = \mathbb{E}[T_n-\theta]\;.$$

L'estimateur est dit sans biais si $B(T_n,\theta)=0$, il est dit asymptotiquement sans biais si $B(T_n,\theta)$ tend vers 0 quand $n$ tend vers l'infini.

Proposition 1.7   L'erreur quadratique de $T_n$ par rapport à $\theta$ est la somme de la variance de $T_n$ et du carré du biais.

Démonstration : Par linéarité de l'espérance on a :

$$\begin{array}{ccc} EQ(T_n,\theta)&=&\mathbb{E}[(T_n-\theta)^2... ...[T_n]])\\ &=& Var[T_n] + (B(T_n,\theta))^2 + 0\;. \end{array}$$

$\square$

Quand un estimateur est sans biais, l'erreur quadratique est égale à la variance. Le critère suivant, conséquence immédiate des propositions 1.5 et 1.7 est souvent utilisé pour démontrer qu'un estimateur est convergent.

Proposition 1.8   Si un estimateur est sans biais ou asymptotiquement sans biais et si sa variance tend vers 0, alors il est convergent.

Quand le biais peut être explicitement calculé, on aura évidemment intérêt à le corriger pour améliorer l'estimateur. Reprenons l'exemple de la loi uniforme sur $[0,\theta]$. Un estimateur naturel de $\theta$ est la plus grande valeur de l'échantillon.

$$T''_n = \max\{X_1,\ldots,X_n\}\;.$$

Comme toutes les valeurs $X_i$ sont inférieures à $\theta$, l'estimateur $T''_n$ sous-estime systématiquement $\theta$. On démontre que son espérance est $n\theta/(n\!+\!1)$ et donc son biais vaut $-\theta/(n\!+\!1)$. On peut corriger le biais en introduisant :

$$T'''_n = \frac{n+1}{n} T''_n\;.$$

Ce nouvel estimateur est sans biais, et il est meilleur que $T''_n$.

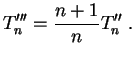
Dans le tableau ci-dessous nous rassemblons les 4 exemples d'estimateurs du paramètre $\theta$ pour la loi uniforme ${\cal U}(0,\theta)$, qui ont été introduits jusqu'ici. Le meilleur des quatre est $T'''_n$.

Estimateur	Biais	Erreur quadratique
$T_n$	0	$\theta^2/(3 n)$
$T'_n$	$\sim \theta/(2 n)$	$\sim \theta^2/n$
$T''_n$	$\sim -\theta/n$	$\sim 2\theta^2/n^2$
$T'''_n$	0	$\sim \theta^2/n^2$

Section : Estimation ponctuelle
Précédent : Estimateurs et estimations
Suivant : Intervalles de dispersion