Le
tableau de contingence
est un moyen particulier de représenter
simultanément deux
caractères
observés sur une même
population,
s'ils sont discrets ou bien continus et regroupés en classes. Les deux
caractères
sont ![]() et
et ![]() , la taille de
l'échantillon
est
, la taille de
l'échantillon
est ![]() . Les
modalités ou classes de
. Les
modalités ou classes de ![]() seront notées
seront notées
![]() , celles de
, celles de ![]() sont notées
sont notées
![]() . On note :
. On note :
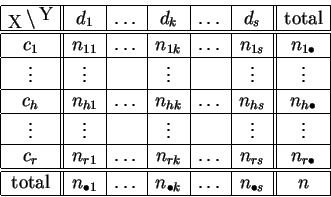
Chaque ligne et chaque colonne correspond à un sous-échantillon
particulier. La ligne d'indice ![]() est la répartition sur
est la répartition sur
![]() des individus pour lesquels le
caractère
des individus pour lesquels le
caractère
![]() prend la valeur
prend la valeur ![]() .
La colonne d'indice
.
La colonne d'indice ![]() est la répartition sur
est la répartition sur
![]() des individus pour lesquels le
caractère
des individus pour lesquels le
caractère
![]() prend la valeur
prend la valeur ![]() . En
divisant les lignes et les colonnes par leurs sommes, on obtient sur chacune
des
distributions empiriques
constituées de
fréquences
conditionnelles.
Pour
. En
divisant les lignes et les colonnes par leurs sommes, on obtient sur chacune
des
distributions empiriques
constituées de
fréquences
conditionnelles.
Pour
![]() et
et
![]() , on les notera :
, on les notera :
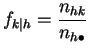 et
et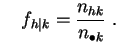
Ces distributions empiriques conditionnelles s'appellent les profils-lignes et profils-colonnes.
L'enjeu principal est d'étudier la dépendance des deux
caractères.
Deux
caractères
sont
indépendants
si la valeur de
l'un n'influe pas sur les distributions des valeurs de l'autre. Si c'est
le cas, les profils-lignes seront tous peu différents de la distribution
empirique de ![]() , et les profils-colonnes de celle de
, et les profils-colonnes de celle de ![]() :
:
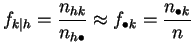 et
et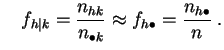
C'est équivalent à dire que les fréquences conjointes doivent être proches des produits de fréquences marginales.
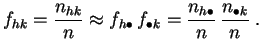
Les
fréquences
conjointes d'une part, et les produits de fréquences
marginales
d'autre part, constituent deux distributions de probabilité
sur l'ensemble produit
![]() .
Un des moyens de quantifier leur proximité est de calculer la
distance du chi-deux
de l'une par rapport à l'autre. Dans ce cas particulier,
on parle de
chi-deux de contingence
.
.
Un des moyens de quantifier leur proximité est de calculer la
distance du chi-deux
de l'une par rapport à l'autre. Dans ce cas particulier,
on parle de
chi-deux de contingence
.
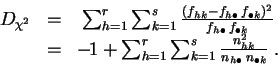
Démonstration : La première expression est l'application directe de la définition 2.7. Pour passer à la seconde, on développe le carré.
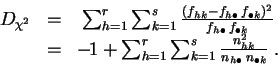
![]()
La
distance du chi-deux
vaut 0 si les deux
caractères
sont
indépendants.
Elle est maximale s'il existe une dépendance systématique.
Supposons ![]() et
et ![]() , pour une certaine fonction bijective
, pour une certaine fonction bijective ![]() . Sur
chaque ligne et chaque colonne du
tableau de contingence,
une seule case est
non nulle, et la
distance du chi-deux
vaut
. Sur
chaque ligne et chaque colonne du
tableau de contingence,
une seule case est
non nulle, et la
distance du chi-deux
vaut ![]() .
.