Valeurs de l'espérance et de la variance

Les hypothèses de modélisation sont ici plus fortes que dans le chapitre précédent. Les données observées sont vues comme des réalisations d'un échantillon de la loi normale ${\cal N}(\mu,\sigma^2)$ , dont l'espérance $\mu$ et la variance $\sigma^2$ sont inconnues. Sous ces hypothèses des résultats théoriques précisent la loi des estimateurs naturels de $\mu$ et $\sigma^2$ que sont la moyenne et la variance empiriques.

Théorème 3.1 Soit $(X_1,\ldots,X_n)$ un échantillon de la loi ${\cal N}(\mu,\sigma^2)$ . On note :

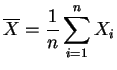$\bullet$: $\overline{X} = \displaystyle{\frac{1}{n} \sum_{i=1}^n X_i}$ la moyenne empirique,
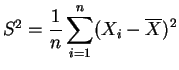$\bullet$: $S^2 = \displaystyle{\frac{1}{n} \sum_{i=1}^n (X_i-\overline{X})^2}$ la variance empirique.

Alors :

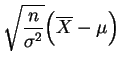$\displaystyle{\sqrt{\frac{n}{\sigma^2}}\Big(\overline{X}-\mu\Big)}$ suit la loi normale ${\cal N}(0,1)$ .
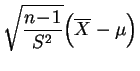$\displaystyle{\sqrt{\frac{n\!-\!1}{S^2}}\Big(\overline{X}-\mu\Big)}$ suit la loi de Student ${\cal T}(n\!-\!1)$ .
$\displaystyle{\frac{nS^2}{\sigma^2}}$ suit la loi du chi-deux ${\cal X}^2(n\!-\!1)$ .

Le point 1) permet de tester des hypothèses portant sur la valeur de $\mu$ , quand $\sigma$ est connu. C'est la situation typique du contrôle de qualité. Considérons une machine destinée à la fabrication de comprimés devant peser 1 gramme. Aucun comprimé, s'il est mesuré au microgramme près, ne pèse 1 gramme exactement. Les poids des comprimés sont en moyenne de 1g, avec un écart-type lié aux caractéristiques de la machine, qui est connu (par exemple $\sigma = 0.01g$ ). Le contrôle de qualité consistera à prélever périodiquement un échantillon de comprimés dont on calcule le poids moyen pour tester qu'il ne s'écarte pas trop de la valeur de référence. Par exemple, si sur un échantillon de 10 comprimés on observe un poids moyen de 0.995, la statistique de test prend la valeur $\sqrt{10}(0.995-1)/0.01 = -1.581$ , dont la p-valeur par rapport à la loi normale ${\cal N}(0,1)$ est :

Si la variance est inconnue, on peut utiliser le point 2) de la même manière. Reprenons les mêmes données en supposant que l'écart-type de 0.01 a été observé. La statistique de test prend la valeur $\sqrt{9}(0.995-1)/0.01 = -1.5$ , dont la p-valeur par rapport à la loi de Student ${\cal T}(9)$ est :

On peut utiliser le point 3) pour tester la valeur de l'écart-type. Toujours sur un échantillon de 10 comprimés, supposons qu'on ait observé un écart-type de 0.013. On souhaite tester si cette valeur est significativement trop grande par rapport à la valeur de référence $\sigma =$ 0.01. La statistique de test prend la valeur

. Pour la loi de chi-deux ${\cal X}^2(9)$ , la p-valeur correspondante est :

On fait souvent l'hypothèse de normalité, sans pouvoir toujours la tester valablement. Dans le cas des grands échantillons on peut s'en dispenser, grâce au théorème central limite

Théorème 3.2 Soit $(X_1,\ldots,X_n)$ un échantillon d'une loi de probabilité d'espérance $\mu$ et de variance $\sigma^2$ finies. Quand

tend vers l'infini, la loi de la variable aléatoire

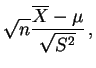
$\displaystyle \sqrt{n}\frac{\overline{X}-\mu}{\sqrt{S^2}}\,,$

converge vers la loi normale ${\cal N}(0,1)$ .

On utilise ce résultat pour tester les valeurs de l'espérance, exactement comme les points 1) et 2) du théorème 3.1.