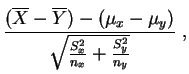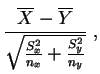Les tests de
Fisher
et
Student
servent à comparer les
moyennes
et les
variances
de deux
échantillons
gaussiens.
Reprenons l'exemple
d'un traitement destiné à diminuer le taux de cholestérol. Des taux
sont mesurés sur une
population
témoin sans traitement, puis sur
des individus après traitement. Le taux moyen après traitement est
inférieur (du moins l'espère-t-on) au taux moyen du groupe témoin.
La question est de savoir si la différence observée est suffisante
pour rejeter
l'hypothèse
![]() que le traitement n'a pas d'effet.
que le traitement n'a pas d'effet.
Pour le modèle probabiliste, on considère deux échantillons indépendants.
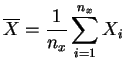 et
et
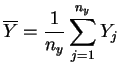 les
moyennes empiriques,
les
moyennes empiriques,
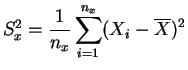 et
et
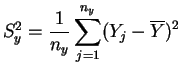 les
variances empiriques.
les
variances empiriques.
Le résultat théorique permettant de comparer les
moyennes empiriques
suppose que l'on fasse l'hypothèse
que les
variances théoriques
![]() et
et
![]() sont égales. Le but du
test de Fisher
est de tester cette
hypothèse
:
sont égales. Le but du
test de Fisher
est de tester cette
hypothèse
:
D'après le théorème 3.1, les rapports des variances empiriques aux variances exactes suivent des lois du chi-deux. Le rapport pondéré de deux variables aléatoires indépendantes suivant des lois du chi-deux suit une loi de Fisher.
La statistique du test de Fisher est :
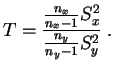
Sous l'hypothèse d'égalité des variances, le théorème suivant permet d'évaluer les différences entre moyennes empiriques.
Ce résultat permet de tester l'hypothèse :
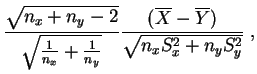
aux
quantiles
de la
loi de Student
![]() . Cette procédure
porte le nom de
test de Student
.
. Cette procédure
porte le nom de
test de Student
.
Supposons que sur les 30 patients du groupe témoin on ait observé un taux de cholestérol moyen de 240mg/dl avec un écart-type de 40mg/dl. Sur les 20 patients du groupe traité, on a observé un taux moyen de 210mg/dl avec un écart-type de 50mg/l. La statistique du test de Fisher prend la valeur 0.690, qui correspond à une p-valeur (pour le test bilatéral) de :
On acceptera donc l'hypothèse d'égalité des variances. La statistique du test de Student prend la valeur 2.30, soit une p-valeur de :
On rejette
![]() au
seuil
au
seuil
![]() 0.05, la baisse est déclarée
significative.
0.05, la baisse est déclarée
significative.
L'hypothèse de normalité, sous laquelle les tests de Fisher et Student sont valides n'est pas toujours vérifiée, ni même vérifiable en pratique. Pour des échantillons de grande taille, le théorème central limite assure la normalité asymptotique des moyennes empiriques. Le résultat suivant ne suppose ni que les échantillons sont gaussiens ni que leurs variances sont égales.