Au paragraphe précédent, nous avons vu comment le test de Student permettait de tester l'effet d'un traitement par comparaison avec un groupe témoin. On peut souhaiter évaluer les effets de plusieurs traitements différents. L'analyse de variance (analysis of variance ou ANOVA) peut être vue comme une généralisation du test de Student.
On souhaite tester les effets de ![]() traitements qui ont été
administrés respectivement à
traitements qui ont été
administrés respectivement à
![]() individus.
En
analyse de variance,
le paramètre susceptible d'influer
sur les
données
étudiées s'appelle un facteur, et ses
valeurs sont les modalités (ici les différents
traitements).
individus.
En
analyse de variance,
le paramètre susceptible d'influer
sur les
données
étudiées s'appelle un facteur, et ses
valeurs sont les modalités (ici les différents
traitements).
Dans le
modèle probabiliste,
chaque modalité correspond à un
échantillon.
Pour
![]() , on note :
, on note :
les
variables aléatoires
modélisant les
données
du ![]() -ième groupe,
supposées
indépendantes
et de même loi
-ième groupe,
supposées
indépendantes
et de même loi
![]() .
On suppose donc en particulier que la
variance
.
On suppose donc en particulier que la
variance
![]() est constante,
hypothèse
qu'un
test
pourra valider.
est constante,
hypothèse
qu'un
test
pourra valider.
On cherche à savoir si la
variabilité observée dans les
données
est uniquement due au hasard,
ou s'il existe effectivement des différences significatives entre les
classes, imputables au facteur. Pour cela, on va
comparer les
variances empiriques
de chaque échantillon,
à la
variance
de l'échantillon
global, de taille
![]() .
La
moyenne
des
variances
(pondérée par les effectifs) résume
la variabilité à l'intérieur des classes, d'où le nom de variance
intra-classes,
ou
variance résiduelle.
La
variance
des
moyennes
décrit les différences entre classes qui peuvent être dues
au traitement, d'où le nom de
variance
inter-classes,
ou
variance
expliquée.
.
La
moyenne
des
variances
(pondérée par les effectifs) résume
la variabilité à l'intérieur des classes, d'où le nom de variance
intra-classes,
ou
variance résiduelle.
La
variance
des
moyennes
décrit les différences entre classes qui peuvent être dues
au traitement, d'où le nom de
variance
inter-classes,
ou
variance
expliquée.
Si les traitements ont effectivement un effet sur les dosages, on s'attend à ce que la variance expliquée soit grande, comparée à la variance résiduelle. La décomposition de la variance de l'échantillon global en variance expliquée et variance résiduelle est explicitée dans le résultat suivant.
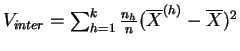 la
variance
des
moyennes
(variance inter-classes),
la
variance
des
moyennes
(variance inter-classes),
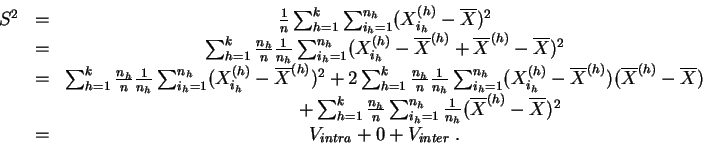
![]()
L'hypothèse à tester est l'égalité des espérances.
Le point 3) du théorème 3.1 permet de quantifier la loi des différentes composantes de la variance, en utilisant le fait que la somme de deux variables indépendantes suivant des chi-deux suit encore une loi du chi-deux, et que leur rapport pondéré suit une loi de Fisher. Les résultats sont les suivants.
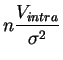 suit la
loi du chi-deux
suit la
loi du chi-deux
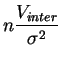 suit la
loi du chi-deux
suit la
loi du chi-deux
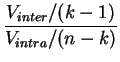 suit la
loi de Fisher
suit la
loi de Fisher
Le
test
ANOVA
consiste donc à rejeter l'égalité des
moyennes
(accepter
qu'il y a un effet des traitements) quand le rapport pondéré
de la
variance expliquée
(inter-classes) à la
variance résiduelle
(intra-classes) est significativement trop grand
par rapport aux
quantiles
de la loi
![]() .
.
Reprenons les
données
sur le taux de cholestérol du paragraphe
précédent. Le facteur a 2 modalités. La
variance expliquée
vaut 2.16, la
variance résiduelle
19.6. Le rapport
pondéré des deux est ![]() , soit une
p-valeur
de :
, soit une
p-valeur
de :
C'est le double de la
p-valeur
que nous avions trouvée pour le
test de Student.
Dans le cas d'une
analyse de variance
à deux modalités,
la
statistique de test
se trouve être le carré de la
statistique
du
test de Student.
Si une
variable aléatoire
suit
la loi
![]() , son carré suit la loi
, son carré suit la loi
![]() .
Effectuer une
analyse de variance
ou un
test de Student
bilatéral
est strictement équivalent.
.
Effectuer une
analyse de variance
ou un
test de Student
bilatéral
est strictement équivalent.
Si
l'analyse de variance
accepte
l'hypothèse
d'égalité des espérances,
l'étude est terminée. Mais si
![]() est rejetée, on peut
souhaiter aller plus loin et comparer les effets du facteur, pour
des sous-ensembles de modalités, en répétant des analyses
de
variance
partielles.
est rejetée, on peut
souhaiter aller plus loin et comparer les effets du facteur, pour
des sous-ensembles de modalités, en répétant des analyses
de
variance
partielles.
On peut présenter
l'analyse de variance
à un facteur
selon un point de vue légèrement différent.
Ecrivons chacune des
variables aléatoires
de l'échantillon
relatif à la ![]() -ième modalité sous la forme :
-ième modalité sous la forme :
Cette présentation a l'avantage d'isoler (dans les paramètres ![]() )
les effets fixes des facteurs. Il est fréquent que l'on ne puisse
pas valider l'hypothèse
d'égalité des
variances, par exemple si
les modalités sont en trop grand nombre ou si les tailles d'échantillons
sont trop petites. On a alors recours à un
modèle
à effets
aléatoires
:
)
les effets fixes des facteurs. Il est fréquent que l'on ne puisse
pas valider l'hypothèse
d'égalité des
variances, par exemple si
les modalités sont en trop grand nombre ou si les tailles d'échantillons
sont trop petites. On a alors recours à un
modèle
à effets
aléatoires
:
Bien que le modèle soit différent, la procédure de test est rigoureusement identique.
L'analyse de variance s'étend à l'étude des effets de plusieurs facteurs. Elle est la base d'un domaine entier de la statistique, la planification d'expérience.