Section : Données bidimensionnelles
Précédent : Représentations bidimensionnelles
Suivant : Régression linéaire simple

Covariance

Si deux caractères quantitatifs $x$ et $y$ sont mesurés sur $n$ individus, on peut considérer l'échantillon bidimensionnel comme un nuage de $n$ points dans $\mathbb{R}^2$. Différentes caractéristiques statistiques permettent de résumer l'information contenue dans sa forme. Si $\overline{x}$ et $\overline{y}$ désignent les moyennes empiriques des deux caractères, le point $(\overline{x},\overline{y})$ est le centre de gravité du nuage. Les variances empiriques $s_x^2$ et $s_y^2$ traduisent la dispersion des abscisses et des ordonnées. Pour aller plus loin dans la description, il faut calculer la covariance.

Définition 3.1   On appelle covariance de $x$ et $y$, et on note $c_{xy}$ la quantité :

$$c_{xy} = \frac{1}{n} \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})\;.$$

Cette définition étend celle de la variance, dans la mesure où $s^2_x = c_{xx}$. La covariance est symétrique ( $c_{xy}=c_{yx}$) et bilinéaire : si $x$ et $x'$ sont deux échantillons de taille $n$, $a$ et $a'$ deux réels et $x^*=ax+a'x'$, alors :

$$c_{x^*y} = ac_{xy} + a' c_{x'y}\;.$$

Comme conséquence de la bilinéarité, on a :

$$s^2_{x+y} = s_x^2 + s_y^2 + 2c_{xy}\;.$$

Pour le calcul pratique, on utilise la formule suivante :

Proposition 3.2   La covariance de $x$ et $y$ s'écrit :

$$c_{xy} = \frac{1}{n} \sum_{i=1}^n x_iy_i\;-\overline{x}\,\overline{y}\;.$$

La covariance est la moyenne des produits moins le produit des moyennes.

Démonstration : Il suffit de développer les produits :

$$\begin{array}{ccc} c_{xy}&=& \frac{1}{n} \sum_{i=1}^n (x_i-\o... ...m_{i=1}^n x_iy_i\Big)-\overline{x}\,\overline{y}\;. \end{array}$$

$\square$

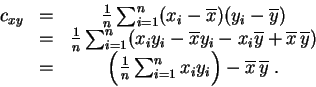
La covariance se compare au produit des écarts-types par l'inégalité de Cauchy-Schwarz.

Proposition 3.3   On a :

$$\vert c_{xy}\vert \leq s_x\,s_y\;.$$ (3.1)

Démonstration : Choisissons une constante $a$ quelconque et calculons la variance de $ax+y$ :

$$s^2_{ax+y} = a^2s_x^2 + 2ac_{xy} + s_y^2\;.$$

Cette quantité est positive ou nulle pour tout $a$. Donc le discriminant de l'expression, vue comme un trinôme en $a$, est nécessairemement négatif. Il vaut :

$$c_{xy}^2 - s_x^2s_y^2\;,$$

d'où le résultat. Remarquons que le discriminant est nul si et seulement si $s^2_{ax+y}$ peut s'annuler, c'est-à-dire s'il existe $a$ tel que $ax+y$ soit constant. Donc l'inégalité 3.1 ne peut être une égalité que s'il existe une relation affine entre $x$ et $y$.$\square$

Au vu de l'inégalité 3.1, il est naturel de diviser la covariance par le produit des écarts-types, pour définir le coefficient de corrélation.

Définition 3.4   On appelle coefficient de corrélation de $x$ et $y$, et on note $r_{xy}$, la quantité :

$$r_{xy} = \frac{c_{xy}}{ s_x\,s_y}\;.$$

Quels que soient l'unité et les ordres de grandeur de $x$ et $y$, le coefficient de corrélation est un nombre sans unité, compris entre -1 et 1. Il traduit la plus ou moins grande dépendance linéaire de $x$ et $y$ ou, géométriquement, le plus ou moins grand aplatissement ne pouvait être une égalité que si $x$ est constant ou si $y$ est de la forme $ax+b$. Si $a$ est positif, le coefficient de corrélation de $x$ avec $ax+b$ est égal à +1, il est égal à -1 si $a$ est négatif. Un coefficient de corrélation nul ou proche de 0 signifie qu'il n'y a pas de relation linéaire entre les caractères. Mais il n'entraîne aucune notion d'indépendance plus générale. Considérons par exemple les deux échantillons :

x	-3	-2	-1	0	1	2	3
y	3	2	1	0	1	2	3.

Leur coefficient de corrélation est nul, et pourtant $x$ et $y$ sont liés par une relation fonctionnelle ($y_i=\vert x_i\vert$).

Quand le coefficient de corrélation est proche de 1 ou -1, les caractères sont dits "fortement corrélés". Il faut prendre garde à la confusion fréquente entre corrélation et causalité. Que deux phénomènes soient corrélés n'implique en aucune façon que l'un soit cause de l'autre. Très souvent, une forte corrélation indique que les deux caractères dépendent d'un troisième, qui n'a pas été mesuré. Ce troisième caractère est appelé "facteur de confusion". Qu'il existe une corrélation forte entre le rendement des impôts en Angleterre et la criminalité au Japon, indique que les deux sont liés à l'augmentation globale de la population. Le prix du blé et la population des rongeurs sont négativement corrélés car les deux dépendent du niveau de la récolte de blé. Il arrive qu'une forte corrélation traduise bien une vraie causalité, comme entre le nombre de cigarettes fumées par jour et l'apparition d'un cancer du poumon. Mais ce n'est pas la statistique qui démontre la causalité, elle permet seulement de la détecter. L'influence de la consommation de tabac sur l'apparition d'un cancer n'est scientifiquement démontrée que dans la mesure où on a pu analyser les mécanismes physiologiques et biochimiques qui font que les goudrons et la nicotine induisent des erreurs dans la reproduction du code génétique des cellules.

Section : Données bidimensionnelles
Précédent : Représentations bidimensionnelles
Suivant : Régression linéaire simple