Dans un problème de régression, les
caractères
ne sont pas considérés
de la même façon. L'un d'eux est le
caractère
"à expliquer", les
autres sont "explicatifs". Nous considérons d'abord le cas de deux
caractères
![]() (explicatif) et
(explicatif) et ![]() (à expliquer). "Expliquer"
signifie ici exprimer une dépendance fonctionnelle de
(à expliquer). "Expliquer"
signifie ici exprimer une dépendance fonctionnelle de ![]() comme fonction
de
comme fonction
de ![]() , de manière à prévoir la valeur de
, de manière à prévoir la valeur de ![]() connaissant celle de
connaissant celle de ![]() .
Si pour tout
individu
.
Si pour tout
individu
![]() ,
,
![]() , et si on
observe une valeur
, et si on
observe une valeur ![]() du
caractère
du
caractère
![]() sur un nouvel
individu,
on donnera
sur un nouvel
individu,
on donnera
![]() comme prédiction du
caractère
comme prédiction du
caractère
![]() sur ce même
individu.
La situation idéale où
sur ce même
individu.
La situation idéale où ![]() n'est jamais rencontrée
en pratique. On cherchera plutôt, dans une famille fixée de fonctions,
quelle est celle pour laquelle les
n'est jamais rencontrée
en pratique. On cherchera plutôt, dans une famille fixée de fonctions,
quelle est celle pour laquelle les ![]() sont les plus proches des
sont les plus proches des ![]() .
La proximité se mesure en général comme une erreur quadratique
moyenne
.
.
La proximité se mesure en général comme une erreur quadratique
moyenne
.
On parle alors de régression au sens des
moindres carrés.
Les différences entre les valeurs observées ![]() et les valeurs
prédites par le
modèle
et les valeurs
prédites par le
modèle
![]() s'appellent les
résidus.
Si le
modèle
est ajusté de sorte que la série des
résidus
soit centrée (de
moyenne
nulle), alors
l'erreur quadratique
s'appellent les
résidus.
Si le
modèle
est ajusté de sorte que la série des
résidus
soit centrée (de
moyenne
nulle), alors
l'erreur quadratique
![]() est la
variance
des
résidus.
La
régression linéaire simple
consiste à chercher
est la
variance
des
résidus.
La
régression linéaire simple
consiste à chercher ![]() parmi les
applications affines. La solution s'exprime simplement à l'aide des
caractéristiques numériques de
parmi les
applications affines. La solution s'exprime simplement à l'aide des
caractéristiques numériques de ![]() et
et ![]() .
.
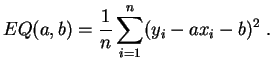
Si
![]() (le
caractère
(le
caractère
![]() n'est pas constant), la fonction
n'est pas constant), la fonction
![]() admet un minimum pour :
admet un minimum pour :
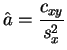 et
etLa valeur de ce minimum est :
Démonstration :Si ![]() est fixé,
est fixé, ![]() est un polynôme de degré 2 en
est un polynôme de degré 2 en ![]() .
Il atteint son minimum pour
.
Il atteint son minimum pour ![]() tel que la dérivée s'annule. Soit :
tel que la dérivée s'annule. Soit :
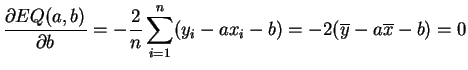
On a donc
![]() .
Reportons cette valeur dans
.
Reportons cette valeur dans ![]() :
:
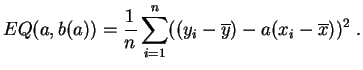
Cette fonction est un polynôme de degré 2 en ![]() , qui atteint
son minimum au point
, qui atteint
son minimum au point ![]() où sa dérivée s'annule, à savoir :
où sa dérivée s'annule, à savoir :
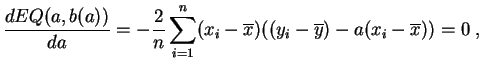
soit en développant :
Posons donc :
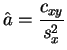 et
et
On a bien pour tout ![]() ,
,
La valeur du minimum est :
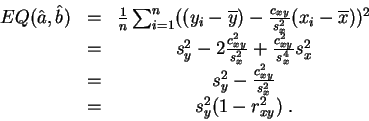
Comme on pouvait s'y attendre
l'erreur quadratique
minimale est d'autant
plus faible que la
corrélation
est forte.![]()
Il est important de noter la dissymétrie des rôles de ![]() et
et ![]() . Par
rapport au
nuage de points,
la droite de régression linéaire
de
. Par
rapport au
nuage de points,
la droite de régression linéaire
de ![]() sur
sur ![]() minimise la somme des distances verticales des points
à la droite. La
droite de régression linéaire
de
minimise la somme des distances verticales des points
à la droite. La
droite de régression linéaire
de ![]() sur
sur ![]() minimise
la somme des distances horizontales. Les deux droites se coupent au
centre de gravité
minimise
la somme des distances horizontales. Les deux droites se coupent au
centre de gravité
![]() du
nuage de points.
L'écart entre les deux est d'autant plus grand que la
corrélation
est faible.
du
nuage de points.
L'écart entre les deux est d'autant plus grand que la
corrélation
est faible.
La prédiction est la première application de la
régression linéaire.
Voici les tailles en centimètres (échantillon ![]() ) et poids en kilogrammes
(
) et poids en kilogrammes
(![]() ) de 10 enfants de 6 ans.
) de 10 enfants de 6 ans.
Les caractéristiques numériques prennent les valeurs suivantes :
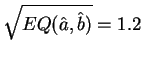 Kg.
Kg.
Comme seconde application, on peut étendre
l'ajustement par quantiles
à
des familles de lois invariantes par transformations affines, comme les lois
normales. Soit ![]() un
échantillon
continu de taille
un
échantillon
continu de taille ![]() dont on souhaite
vérifier qu'il pourrait être issu d'une
loi normale
dont on souhaite
vérifier qu'il pourrait être issu d'une
loi normale
![]() , les paramètres
, les paramètres ![]() et
et ![]() étant inconnus. Pour
étant inconnus. Pour
![]() , notons comme d'habitude
, notons comme d'habitude ![]() les
statistiques d'ordre.
Si l'hypothèse
de normalité est pertinente,
alors
les
statistiques d'ordre.
Si l'hypothèse
de normalité est pertinente,
alors ![]() doit être proche du quantile
doit être proche du quantile
![]() de la loi
de la loi
![]() .
Rappelons que si une
variable aléatoire
.
Rappelons que si une
variable aléatoire
![]() suit la loi
suit la loi
![]() ,
alors
,
alors
![]() suit la loi
suit la loi
![]() . Ceci revient
à dire que pour tout
. Ceci revient
à dire que pour tout
![]() :
:
Notons
![]() les valeurs
de la
fonction quantile
de la loi
les valeurs
de la
fonction quantile
de la loi
![]() aux points
aux points ![]() .
Si l'hypothèse
de normalité est vérifiée, les points de
coordonnées
.
Si l'hypothèse
de normalité est vérifiée, les points de
coordonnées
![]() devraient être proches de la droite
d'équation
devraient être proches de la droite
d'équation
![]() . Une
régression linéaire
des
. Une
régression linéaire
des ![]() sur
les
sur
les ![]() fournit à la fois une
estimation
de
fournit à la fois une
estimation
de ![]() et
et ![]() et une
indication sur la qualité de
l'ajustement.
Avant les logiciels de calcul, on
vendait du papier "gausso-arithmétique", gradué en abscisses selon les
quantiles
de la loi
et une
indication sur la qualité de
l'ajustement.
Avant les logiciels de calcul, on
vendait du papier "gausso-arithmétique", gradué en abscisses selon les
quantiles
de la loi
![]() . Il suffisait de reporter en ordonnée
les valeurs des
. Il suffisait de reporter en ordonnée
les valeurs des ![]() pour tracer à la main la droite de régression
linéaire, qui porte le nom de
"droite de Henry", du nom du colonel qui a inventé cette méthode au
siècle dernier pour étudier la portée des canons.
pour tracer à la main la droite de régression
linéaire, qui porte le nom de
"droite de Henry", du nom du colonel qui a inventé cette méthode au
siècle dernier pour étudier la portée des canons.
Le problème de la régression est de déterminer, dans une famille de fonctions donnée, quelle est celle qui minimise l'erreur quadratique (3.2). Or il est fréquent qu'il n'y ait pas de solution explicite. Pour certaines familles de fonctions, on transforme le problème de manière à se ramener à une régression linéaire. Voici quelques cas fréquents.
Comme exemple d'application, nous reprenons le problème de
l'ajustement par les quantiles,
pour la famille des lois de
Weibull,
qui sont souvent
utilisées pour modéliser des durées de survie ou des durées
de fonctionnement en fiabilité. La
fonction quantile
de la loi de Weibull
![]() est :
est :
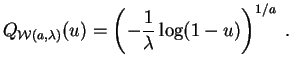
Soit ![]() un
échantillon
que l'on souhaite ajuster par une
loi de Weibull,
de paramètres
un
échantillon
que l'on souhaite ajuster par une
loi de Weibull,
de paramètres ![]() et
et ![]() inconnus.
Pour
inconnus.
Pour
![]() , la
statistique d'ordre
, la
statistique d'ordre
![]() doit être proche
du
quantile
doit être proche
du
quantile
![]() .
.
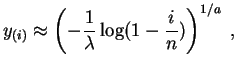
soit :
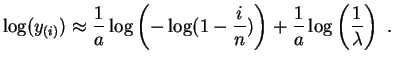
Posons
![]() et
et
![]() . Les points
. Les points
![]() devraient être proches de la droite d'équation
devraient être proches de la droite d'équation
![]() . Une
régression linéaire
fournira
non seulement des valeurs pour
. Une
régression linéaire
fournira
non seulement des valeurs pour ![]() et
et ![]() , mais aussi une indication
sur la qualité de
l'ajustement.
Avant les logiciels de calcul, il
existait du "papier
Weibull",
gradué de manière à automatiser
ce cas particulier de régression non linéaire.
, mais aussi une indication
sur la qualité de
l'ajustement.
Avant les logiciels de calcul, il
existait du "papier
Weibull",
gradué de manière à automatiser
ce cas particulier de régression non linéaire.